Cho hình thang vuông ABCD ( ), có CD = 2AB, gọi H là hình chiếu của D trên AC, M là trung điểm của HC. Chứng minh .
Câu hỏi:
Cho hình thang vuông ABCD (), có CD = 2AB, gọi H là hình chiếu của D trên AC, M là trung điểm của HC. Chứng minh .
Trả lời:
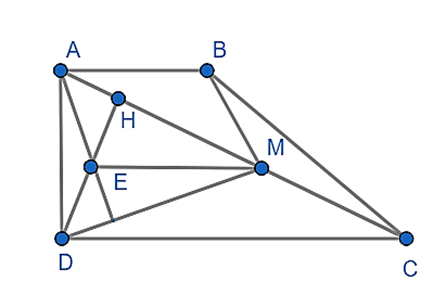
Gọi E là trung điểm HD
Ta có: EM là đường trung bình của tam giác HDC
Nên: EM // DC và EM =
Xét tứ giác ABME có: AB // EM // CD
AB = EM
Nên ABME là hình bình hành
Suy ra: BM // AE (1)
Lại có: Xét trong tam giác ADM có: DH ⊥ AM (giả thiết); EM ⊥ AD (vì AD ⊥ AB mà AB // EM)
Nên E là trực tâm của tam giác ADM
Suy ra: AE ⊥ DM (2)
Từ (1) và (2): BM ⊥ DM hay .

