Cho hình vẽ. Chứng minh rằng: a) tam giác AOD = tam giác COB
Câu hỏi:
Cho hình vẽ. Chứng minh rằng:
a) ∆AOD = ∆COB.
b) AD // BC.
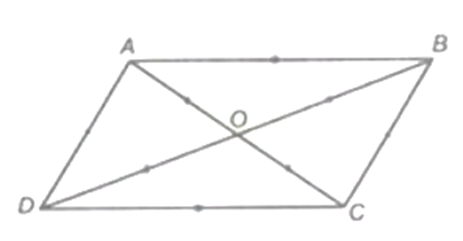
Trả lời:
a) Theo hình vẽ ta có: OA = OB = OC = OD
AC cắt BD tại trung điểm O
Suy ra: ABCD là hình bình hành
Xét ∆AOD và ∆COB có:
AO = BO = \(\left( {\frac{1}{2}AC = \frac{1}{2}BD} \right)\)
OD = OC
AD = BC (theo hình)
Suy ra: ∆AOD = ∆COB (c.c.c)
b) Theo phần a có: ∆AOD = ∆COB nên \(\widehat {ADO} = \widehat {OBC}\)
Mà 2 góc này ở vị trí so le trong nên AD // BC.

