Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng phía đối với AB. Từ điểm M trên đường tròn (M khác A; B)
Câu hỏi:
Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng phía đối với AB. Từ điểm M trên đường tròn (M khác A; B) vẽ tiếp tuyến với nửa đường tròn, cắt Ax và By lần lượt tại C và D.
a) Chứng minh .
b) Chứng minh AC.BD không đổi.
Trả lời:
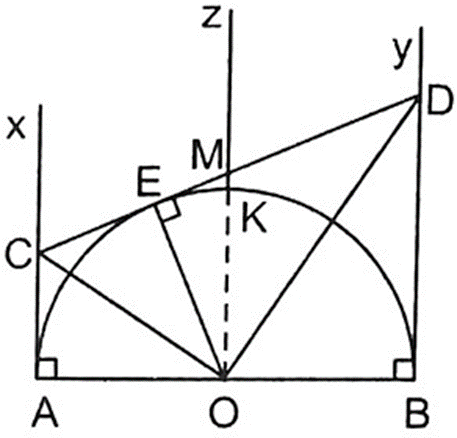
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
• OC là tia phân giác của
• OD và tia phân giác của
Khi đó, OC và OD là các tia phân giác của hai góc kề bù và
Do đó OC ⊥ OD.
Vậy (đpcm)
b) Ta có: AC = CM, BD = DM nên AC . BD = CM . MD.
Xét ΔCOD vuông tại O, ta có:
CM . MD = OM2 = R2 (R là bán kính đường tròn O).
Vậy AC . BD = R2 (không đổi).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Chứng minh rằng A = 1.5 + 2.6 + 3.7 + … + 2023.2027 chia hết cho 11, 23 và 2023.
Xem lời giải »
Câu 4:
Cho hình bình hành ABCD. Gọi E và F theo thứ tự là trung điểm của AB và CD
a) Chứng minh rằng AF // CE.
b) Gọi M, N theo thứ tự là giao điểm của BD và AF, CE. Chứng minh rằng DM = MN = NB.
Xem lời giải »
Câu 5:
Cho tam giác ABC( AB < AC ) có hai đường phân giác CM, BN cắt nhau ở D. Qua A kẻ AE và AF vuông góc với BN và CM. Các đường thẳng AE và AF cắt BC ở I; K.
a) Chứng minh AFDE nội tiếp.
b) Chứng minh AB.NC = AN.BC.
Xem lời giải »
Câu 6:
Cho tam giác ABC có đường cao AH và BD cắt nhau tại I.
a) Chứng minh 4 điểm C, D, I, H cùng thuộc 1 đường tròn.
b) Chứng minh 4 điểm A, B, H, D cùng thuộc 1 đường tròn.
c) Tính bán kính đường tròn đi qua 4 điểm C, D, H, I nếu biết CH = 4cm và = 30°.
Xem lời giải »
Câu 7:
Cho tam giác vuông ABC vuông ở A có đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB và AC.
a. So sánh AH và EF.
b. Tính độ dài HF biết AB = 6 cm, BC = 10 cm và BH = 3,6 cm.
Xem lời giải »


