Cho tam giác ABC có đường cao AH và BD cắt nhau tại I. a) Chứng minh 4 điểm C, D, I, H cùng thuộc 1 đường tròn. b) Chứng minh 4 điểm A, B, H, D cùng thuộc 1 đường tròn.
Câu hỏi:
Cho tam giác ABC có đường cao AH và BD cắt nhau tại I.
a) Chứng minh 4 điểm C, D, I, H cùng thuộc 1 đường tròn.
b) Chứng minh 4 điểm A, B, H, D cùng thuộc 1 đường tròn.
c) Tính bán kính đường tròn đi qua 4 điểm C, D, H, I nếu biết CH = 4cm và = 30°.
Trả lời:
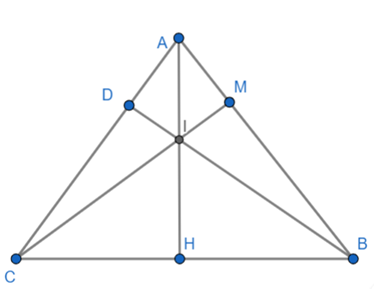
a) Xét tam giác DIC vuông tại D (BD ⊥ AC)
⇒ D, I, C cùng thuộc đường tròn đường kính IC
Xét tam giác HIC vuông tại H (AH ⊥ BC)
⇒ H, I, C cùng thuộc đường tròn đường kính IC
Vậy D, I, C, H cùng thuộc đường tròn đường kính IC
b) Xét tam giác ABH vuông tại H (AH ⊥ BC)
⇒ A, B, H cùng thuộc đường tròn đường kính AB
Xét tam giác ABD vuông tại D (BD ⊥ AC)
⇒ A, B, D cùng thuộc đường tròn đường kính AB
Vậy A, B, H, D cùng thuộc đường tròn đường kính AB
c) Gọi M là giao điểm của CI và AB
Xét tam giác BAC có: AH và BD là đường cao, AH ∩ BD ={I}
Nên I là trực tâm của tam giác BAC
Vậy AM là đường cao thứ 3 của tam giác ABC
Xét ∆ABH và ∆CBM có:
chung
⇒ ∆ABH ~ ∆CBM (g.g)
⇒ = 30°
Xét ∆HCI vuông tại H có: cos
Mà đường tròn đi qua D, I, C, H là đường tròn đường kính IC
Suy ra bán kính đường tròn là

