Cho phương trình (4log2^2x+logx-5)căn 7^x-m =0 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để

Câu hỏi:

Cho phương trình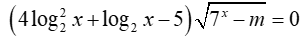 Cho phương trình (4log2^2x+logx-5)căn 7^x-m =0 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để (ảnh 1) ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt

A. 49

B. 49

C. vô số

D. 48

Trả lời:

Chọn B

Điều kiện: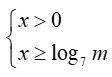 Cho phương trình (4log2^2x+logx-5)căn 7^x-m =0 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để (ảnh 2)

Với m=1, phương trình trở thành 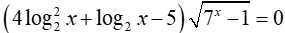Cho phương trình (4log2^2x+logx-5)căn 7^x-m =0 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để (ảnh 3)

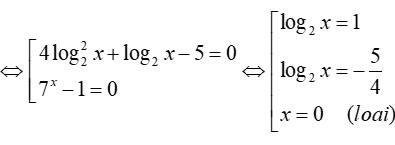
Cho phương trình (4log2^2x+logx-5)căn 7^x-m =0 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để (ảnh 4)

Phương trình này có hai nghiệm (thỏa)

Với $m \geq 2$ , điều kiện phương trình là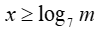 Cho phương trình (4log2^2x+logx-5)căn 7^x-m =0 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để (ảnh 5)

Pt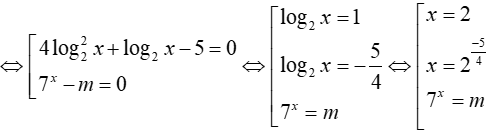 Cho phương trình (4log2^2x+logx-5)căn 7^x-m =0 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để (ảnh 6)

Do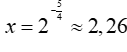 Cho phương trình (4log2^2x+logx-5)căn 7^x-m =0 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để (ảnh 7) không là số nguyên, nên phương trình có đúng 2 nghiệm khi và chỉ khi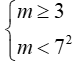

(nghiệm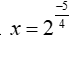 Cho phương trình (4log2^2x+logx-5)căn 7^x-m =0 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để (ảnh 9) không thỏa điều kiện và nghiệm x=2 thỏa điều kiện và khác )

Vậy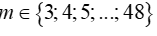 Cho phương trình (4log2^2x+logx-5)căn 7^x-m =0 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để (ảnh 10) . Suy ra có 46 giá trị của m .

Do đó có tất cả 47 giá trị của m

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Với a là số thực dương tùy ý,

\log_{2} 2 a

bằng

Xem lời giải »

Câu 2:

Nghiệm của phương trình $\log_{2} (x + 6) = 5$ là

Xem lời giải »

Câu 3:

Với

a, b

là các số thực dương tùy ý thỏa mãn

\log_{3} a - 2 \log_{9} b = 3

, mệnh đề nào dưới đây đúng?

Xem lời giải »

Câu 4:

Tập nghiệm của bất phương trình $\log_{3} (36 - x^{2}) \geq 3$ là

Xem lời giải »

Câu 5:

Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình $16^{x} - m {.4}^{x + 1} + 5 m^{2} - 45 = 0$ có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử?

Xem lời giải »

Câu 6:

Cho $a > 0$ , $b > 0$ thỏa mãn $\log_{3 a + 2 b + 1} (9 a^{2} + b^{2} + 1) + \log_{6 a b + 1} (3 a + 2 b + 1) = 2$ . Giá trị của $a + 2 b$ bằng

Xem lời giải »

Câu 7:

Cho phương trình $5^{x} + m = \log_{5} (x - m)$ với m là tham số. Có bao nhiêu giá trị nguyên của $m \in (- 20; 20)$ để phương trình đã cho có nghiệm?

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Cho phương trình (4log2^2x+logx-5)căn 7^x-m =0 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để

Xem thêm bài tập Toán có lời giải hay khác: