Cho phương trình mặt phẳng (P): 2x+y+z-3=0, đường thẳng d': (x-1)/1=y/2
Câu hỏi:
Cho phương trình mặt phẳng (P): 2x+y+z-3=0, đường thẳng và điểm . Viết phương trình đường thẳng d đi qua A, nằm trong (P) sao cho khoảng cách d và d' đạt giá trị lớn nhất.
B. .
C. .
D. .
Trả lời:
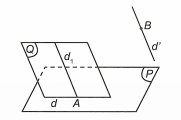
Gọi là đường thẳng đi qua A và song song với d'.
Phương trình của là: .
Trên đường thẳng lấy điểm .
Gọi là mặt phẳng chứa d và .
Ta có .
Do cố định cho nên .
Đẳng thức xảy ra khi và chỉ khi trong đó H là hình chiếu của B lên .
Ta tìm được nên .
Ta có .
Vậy phương trình của đường thẳng d là .
Chọn A.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Viết phương trình đường thẳng d đi qua điểm A(1,1,-1) cho trước, nằm trong mặt phẳng và cách điểm một khoảng lớn nhất.
Xem lời giải »
Câu 2:
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(2,1,-2), B(5,1,1) và mặt cầu . Xét đường thẳng d đi qua A và tiếp xúc với (S) sao cho khoảng cách từ B đến d nhỏ nhất. Phương trình của đường thẳng d là
Xem lời giải »
Câu 3:
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm . Khoảng cách giữa AB và CD là
Xem lời giải »
Câu 4:
Cho phương trình mặt phẳng (P): 2x+y+z-3=0, đường thẳng và điểm . Viết phương trình đường thẳng d đi qua A, nằm trong (P) sao cho khoảng cách d và d' đạt giá trị lớn nhất.
Xem lời giải »
Câu 5:
Trong không gian Oxyz, cho điểm P(a,b,c). Khoảng cách từ điểm P đến trục tọa độ Oy bằng
Xem lời giải »
Câu 6:
Trong không gian Oxyz, khoảng cách giữa đường thẳng và mặt phẳng bằng
Xem lời giải »
Câu 7:
Trong không gian Oxyz, khoảng cách giữa hai đường thẳng và bằng
Xem lời giải »


