Viết phương trình đường thẳng d đi qua điểm A(1,1,-1) cho trước, nằm trong mặt
Câu hỏi:
A. .
Trả lời:
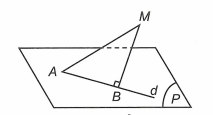
Ta gọi B là hình chiếu của M lên đường thẳng d khi đó .
Suy ra nên đường thẳng d đi qua điểm A và vuông góc với MA.
Đồng thời đường thẳng d nằm trong mặt phẳng nên ta có
Chọn C.

