Cho số phức z = (1 - i) ( 2i - 8) . Tìm số phức w = iz+ z ngang

Câu hỏi:

Cho số phức z = (1 - i) ( 2i - 8) . Tìm số phức $w = i z + \bar{z}$

A. w = 10 - 10i.

B. w = -3 - 3i.

C. w = 16 - 16i.

D. w = -16 - 16i.

Trả lời:

Chọn D.

+ Do z = (1 - i)(2i - 8) = 2i + 2 - 8 + 8i hay z = -6 + 10i

Khi đó: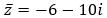và iz = -10 - 6i

Khi đó: w = ( -10 - 6i) + ( -6 -10i) = -16 - 16i.

Câu 1:

Cho hai số phức z₁= 3i - 2; z₂ = 5 + 3i. Tìm số phức z = z₁ + z₂.

Câu 2:

Cho số phức z = a + bi và $w = \frac{1}{2} (z + \bar{z})$ . Mệnh đề sau đây là đúng?

Câu 3:

Cho hai số phức z₁ = 2 - 3i; z₂= 4i - 10. Tìm số phức z = z₁ – z₂.

Câu 4:

Cho hai số phức z = a + bi và z’ = a’ + b’i . Tìm điều kiện giữa a; b; a’; b’ để z + z’ là một số thuần ảo.

Câu 5:

Cho số phức z = ( 2 + i)( 3 - i). Tìm phần thực a và phần ảo b của số phức $\bar{z}$

Câu 6:

Tìm số phức liên hợp của số phức $z = \frac{1 + i}{2 - i}$

Câu 7:

Tìm số phức z thỏa mãn $z - (2 + 3 i) \bar{z} = 1 - 9 i$

Câu 8:

Cho số phức $z = \frac{4 - 8 i}{1 + i}$ . Tìm phần thực a và phần ảo b của số phức $\bar{z}$

Các dạng bài tập Toán lớp 12