Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc AC, từ B kẻ tia By song song AC
Câu hỏi:
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc AC, từ B kẻ tia By song song AC. Gọi M là giao điểm của tia Ax và tia By. Nối M là trung điểm P của AB, đường thẳng MP cắt AC tại Q và đường thẳng BQ cắt AI tại H
a) Tứ giác AMBQ là hình gì?
b) Chứng minh CH vuông góc AB
c) Chứng minh tam giác PIQ cân
Trả lời:
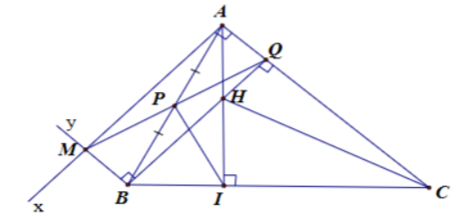
a) AM vuông góc AC và BM // AC nên AM ⊥ BM
Xét AMBQ có:
Nên AMBQ là hình chữ nhật
b, AMBQ là hình chữ nhật nên BQ⊥AC mà BQ ∩ AI = H
Suy ra H là trực tâm của tam giác ABC
Do đó: CH⊥ AB
c, Tam giác ABI vuông tại I có đường trung tuyến IP nên
Do AMBQ là hình chữ nhật nên
Suy ra IP = PQ
Hay tam giác IPQ cân tại P

