Cho tam giác ABC có góc B = góc C = 40 độ. Kẻ phân giác

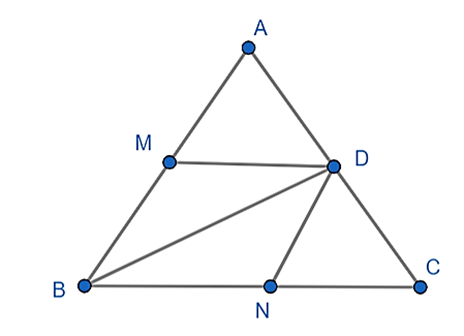
Kẻ MD // BC (M thuộc AB)

Lấy N thuộc BC sao cho BD = BN

Trong tam giác DBN có $\widehat {DBN} = \frac{1}{2}\widehat B = 20^\circ$(BD là phân giác)

Mà BD = BN nên tam giác BDN cân tại B; $\widehat {BND} = \widehat {BDN}$

Suy ra: $\widehat {BND} = \frac{{180^\circ - 20^\circ }}{2} = 80^\circ$

Mà $\widehat {DNB}$là góc ngoài của tam giác DNC

Nên: $\widehat {DNB} = \widehat C + \widehat {CDN}$

⇒ $\widehat {CDN} = \widehat {DNB} - \widehat C = 80^\circ - 40^\circ = 40^\circ$

Vì MD // BC nên $\widehat {MDB} = \widehat {DBN} = 20^\circ$

Thấy tam giác BMD cân tại M vì $\widehat {MBD} = \widehat {MDB} = \widehat {DBN} = 20^\circ$

Suy ra: BM = MD

Lại có: MD // BC

Suy ra: BM = DC

Mà AB = AC nên AM = AD

$\widehat {ABD} = \widehat {DBC}$ = $\frac{1}{2}\widehat B = 20^\circ$

$\widehat {ADB} = 180^\circ - 20^\circ - 100^\circ = 60^\circ$

$\widehat {BDC} = 180^\circ - 20^\circ - 40^\circ = 120^\circ$

Vì BDN là tam giác cân tại B nên $\widehat {BDN} = \widehat {BND} = \frac{{180^\circ - 20^\circ }}{2} = 80^\circ$

Suy ra: $\widehat {NDC} = \widehat {BDC} - \widehat {BDN} = 120^\circ - 80^\circ = 40^\circ$

Mà $\widehat {DCN} = 40^\circ$

Nên tam giác DCN cân tại N.

⇒ DN = NC

Xét tam giác AMD và tam giác DNC có:

$\widehat {ADM} = \widehat {DCN}$(2 góc đồng vị)

$\widehat {AMD} = \widehat {NDC} = 40^\circ$

⇒ ∆AMD ∽ ∆ NDC (g.g)

⇒ $\frac{{AM}}{{DN}} = \frac{{AD}}{{NC}} = \frac{{MD}}{{DC}}$

Suy ra: AD = CN.

Vậy BD + AD = BD + NC = BN + NC = BC.