Cho tam giác ABC đều. Trên tia đối của AB lấy điểm D, trên tia đối của BC lấy điểm E, trên tia đối của CA lấy điểm F sao cho AD = BE = CF. Chứng minh rằng tam giác DEF đều.
Câu hỏi:
Cho tam giác ABC đều. Trên tia đối của AB lấy điểm D, trên tia đối của BC lấy điểm E, trên tia đối của CA lấy điểm F sao cho AD = BE = CF. Chứng minh rằng tam giác DEF đều.
Trả lời:
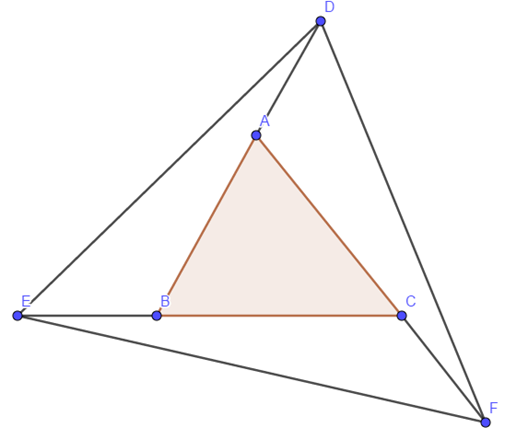
Xét tam giác EBD và tam giác FCE có:
EC = DB (vì AB = BC; AD = EB nên EB + BC = AB + AD)
(cùng là 2 góc ngoài của 1 tam giác đều)
EB = FC (giả thiết)
Suy ra: ∆EBD = ∆FCE (c.g.c)
⇒ DE = EF (1)
Chứng minh tương tự: ∆EBD = ∆DAF (c.g.c)
⇒ DE = FD (2)
Từ (1) và (2): DE = DF = EF
Vậy tam giác DEF đều.

