Cho tam giác ABC, kẻ tia phân giác Bx của góc B, Bx cắt tia AC
Câu hỏi:
Cho tam giác ABC, kẻ tia phân giác Bx của góc B, Bx cắt tia AC tại M. Từ M kẻ đường thẳng song song với AB, nó cắt BC tại N. Từ N kẻ tia NY // Bx. Chứng minh:
a. \(\widehat {xAB} = \widehat {BMN}\).
b. Tia Ny là tia phân giác của góc MNC.
Trả lời:
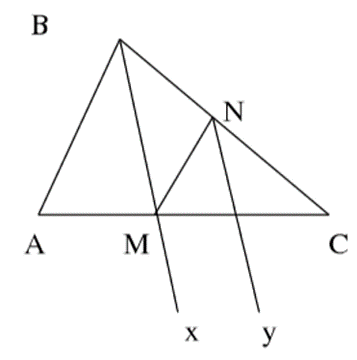
a) Trong tam giác ABC tại đỉnh B có:
\(\widehat {ABx\;} = \widehat {xBC}\)(vì Bx là tia phân giác của góc B)
\(\widehat {BMN} = \widehat {ABx}\)(2 góc so le trong vì MN//BA)
Vậy \(\widehat {BMN} = \widehat {xBC}\).
b) \[\widehat {BMN\;} = \widehat {MNy}\](2 góc so le trong vì Ny//Bx)
\(\widehat {xBC} = \widehat {yNC}\)(2 góc đồng vị vì Ny//Bx)
Vậy \[\widehat {yNC} = \widehat {MNy}\]mà tia Ny là tia nằm giữa hai tia MN và NC
Do đó: Ny là tia phân giác của MNC.

