o tam giác ABC, IG vuông góc với IC trong đó I là tâm đường tròn
Câu hỏi:
Cho tam giác ABC, IG vuông góc với IC trong đó I là tâm đường tròn nội tiếp, G là trọng tâm. Chứng minh \(\frac{{a + b + c}}{3} = \frac{{2ab}}{{a + b}}\).
Trả lời:
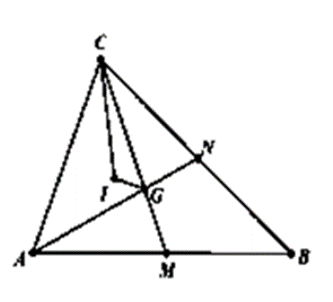
Ta chứng minh \(a\overrightarrow {IA} + b\overrightarrow {IB} + c\overrightarrow {IC} = \overrightarrow 0 \)
⇒ \(a\left( {\overrightarrow {IC} + \overrightarrow {CA} } \right) + b\left( {\overrightarrow {IC} + \overrightarrow {CB} } \right) + c\overrightarrow {IC} = \overrightarrow 0 \)
⇒ \(\overrightarrow {CI} = \frac{1}{{a + b + c}}\left( {a.\overrightarrow {CA} + b.\overrightarrow {CB} } \right)\)
⇒ \(\overrightarrow {GI} = \overrightarrow {CI} - \overrightarrow {CG} = \left( {\frac{a}{{a + b + c}} - \frac{1}{3}} \right)\overrightarrow {CA} + \left( {\frac{b}{{a + b + c}} - \frac{1}{3}} \right)\overrightarrow {CB} \)
Khi đó: ⇔ \(\left[ {\left( {2a - b - c} \right)\overrightarrow {CA} + \left( {2b - a - c} \right)\overrightarrow {CB} } \right]\left( {a\overrightarrow {CA} + b\overrightarrow {CB} } \right) = \overrightarrow 0 \)
⇔ \(\left( {ab + \overrightarrow {CA} .\overrightarrow {CB} } \right)\left[ {b\left( {2a - b - c} \right) + a\left( {2b - a - c} \right)} \right] = 0\)
Do \(\left( {ab + \overrightarrow {CA} .\overrightarrow {CB} } \right) = ab + ab\cos C = ab\left( {1 + \cos C} \right) > 0\)
Nên ta có: b(2a – b – c) + a(2b – a – c) = 0
⇔ b(3a – a – b – c) + a(3b – a – b – c) = 0
⇔ 6ab = (a + b)(a + b + c)
⇔ \(\frac{{a + b + c}}{3} = \frac{{2ab}}{{a + b}}\).

