Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Điểm M nằm giữa B và C, gọi I là trung điểm của AC, lấy điểm N đối xứng M qua I.
Câu hỏi:
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Điểm M nằm giữa B và C, gọi I là trung điểm của AC, lấy điểm N đối xứng M qua I.
a) Tính độ dài cạnh BC?
b) Tứ giác AMCN là hình gì? Vì sao?
Trả lời:
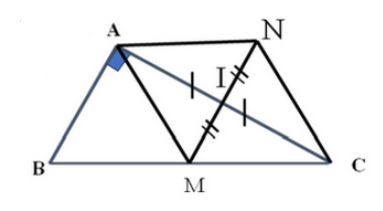
Ta có tam giác ABC vuông tại A, với AB = 6cm và AC = 8cm.
Sử dụng định lý Pythagoras, ta có: BC2 = AB2 + AC2 = 62 + 82 = 100
Suy ra: BC = 10 cm
Vậy độ dài cạnh BC là 10cm.
b) Vì N là điểm đối xứng của M qua I, nên ta có AI = IN và AM = MN.
Đồng thời, ta có IM = IN (tính chất đối xứng); IA = IC
Vậy ta có 2 đường chéo cắt nhau tại trung điểm mỗi đường
Điều này chứng tỏ AMCN là hình bình hành.

