Cho tam giác ABC vuông tại A. M là trung điểm BC, D đối xứng với A
Câu hỏi:
Cho tam giác ABC vuông tại A. M là trung điểm BC, D đối xứng với A qua M.
a) Chứng minh ABCD là hình chữ nhật.
b) Lấy E đối xứng với A qua C. O là trung điểm CD. Chứng minh B đối xứng với E qua O.
Trả lời:
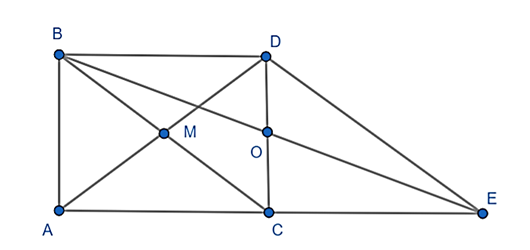
a) Vì ABC là tam giác vuông tại A có AM là đường trung tuyến nên AM = \(\frac{1}{2}BC = BM = MC\)
Lại có: D là đối xứng của A qua M nên MA = MD
Suy ra: MA = MD = MB = MC hay BC và AD cắt nhau tại trung điểm M mỗi đường
⇒ ABCD là hình bình hành
Mà \(\widehat {BAC} = 90^\circ \)
⇒ ABCD là hình chữ nhật
b) Vì ABCD là hình chữ nhật nên BD // AC và BD = AC
Suy ra: BD // CE (1)
E là đối xứng của A qua C nên AC = CE
Mà AC = BD nên BD = CE (2)
Từ (1) và (2): BDEC là hình bình hành
⇒ DC và BE cắt nhau tại trung điểm mỗi đường
Mà O là trung điểm DC nên O là trung điểm BE
Vậy E đối xứng với B qua O.

