Cho tam giác ABC vuông tại A trung tuyến AD. Kẻ DM vuông góc AB (M thuộc AB), kẻ DN vuông góc AC (N thuộc AC). a) ANDM là hình gì? b) Lấy E đối xứng Dqua M. Chứng minh rằng AE//MN. c) D nằm ở
Câu hỏi:
Cho tam giác ABC vuông tại A trung tuyến AD. Kẻ DM vuông góc AB (M thuộc AB), kẻ DN vuông góc AC (N thuộc AC).
a) ANDM là hình gì?
b) Lấy E đối xứng Dqua M. Chứng minh rằng AE//MN.
c) D nằm ở vị trí nào trên cạnh BC để ANDM là hình chữ nhật.
Trả lời:
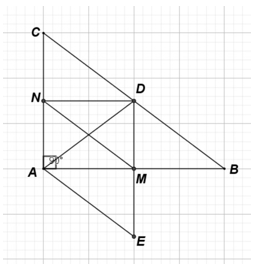
a) Xét tứ giác ANDM có 3 góc vuông tại A, M, N
⇒ ANDM là hình chữ nhật
Vậy ANDM là hình chữ nhật
b) Vì ANDM là hình chữ nhật
⇒ AN = DM; AN//DM
Lại có E đối xứng với D qua M
⇒ DM = ME
⇒ ME // AN; ME = AN
⇒ ANME là hình bình hành
⇒ AE // MN
Vậy AE // MN
c) D nằm ở vị trí nào thì ANDM đều là hình chữ nhật.


