Cho tam giác DEF cân tại D. Trên DE lấy điểm M, trên DF lấy điểm N sao cho DM = DN. Chứng minh tứ giác MNFE là hình thang cân.
Câu hỏi:
Cho tam giác DEF cân tại D. Trên DE lấy điểm M, trên DF lấy điểm N sao cho DM = DN. Chứng minh tứ giác MNFE là hình thang cân.
Trả lời:
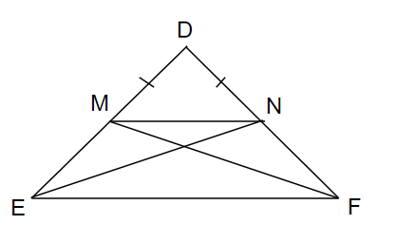
Ta có △DEF cân tại D
⇒ DE = DF
Xét △DNE và △DMF ta có:
DE = DF (gt)
góc chung
DM = DN (gt)
⇒ △DNE = △DMF (c.g.c)
⇒ EN = FM
Suy ra: MNFE là hình thang cân (dấu hiệu nhận biết hình thang cân).


