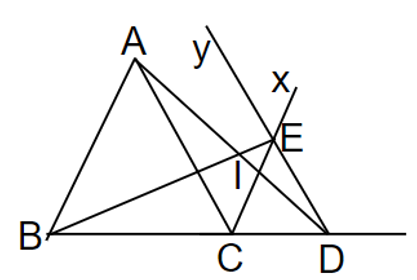
Cho tam giác đều ABC. Trên tia đối của tia CB lấy điểm D. Trong nửa mặt phẳng bờ BC chứa điểm A kẻ các tia Cx // AB, Dy // AC. Hai tia này cắt nhau tại E. Chứng minh rằng: a) Tam giác ECD đều

Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho $\overrightarrow{BH}=\frac{1}{3}\overrightarrow{HC}$. Điểm M di động nằm trên BC sao cho $\overrightarrow{BM}=x\overrightarrow{BC}$. Tìm x sao cho độ dài của $\overrightarrow{MA}+\overrightarrow{GC}$ đạt giá trị nhỏ nhất.

Cho tam giác ABC có $\widehat{A}=70°$, các đường phân giác BD, CE cắt nhau ở I. Tính $\widehat{BIC}$

Cho tam giác ABC có $\widehat{C}=90°$. Kẻ đường cao CH. Biết HB - HA = AC. Tính $\widehat{A},\widehat{B}$.

Cho tam giác ABC có góc C nhọn, AH và BK là hai đường cao, HK = $\sqrt{7}$, diện tích tứ giác ABHK bằng 7 lần diện tích tam giác CHK. Khi đó bán kính đường tròn ngoại tiếp tam giác ABC bằng?

Cho tam giác ABC vuông tại A trung tuyến AD. Kẻ DM vuông góc AB (M thuộc AB), kẻ DN vuông góc AC (N thuộc AC).

a) ANDM là hình gì?

b) Lấy E đối xứng Dqua M. Chứng minh rằng AE//MN.

c) D nằm ở vị trí nào trên cạnh BC để ANDM là hình chữ nhật.

Cho tam giác ABC vuông cân tại A và điểm M thuộc cạnh BC. Chứng minh MB² + MC² = 2MA².

Cho tam giác ABC vuông cân tại A. Biết AB = AC = 4cm.

a, Tính BC.

b, Từ A kẻ AD vuông góc BC tại D. Chứng minh D là trung điểm BC.

c, Từ D kẻ DE vuông góc AC tại E. Chứng minh tam giác AED vuông cân.

d, Tính AD.

Cho ABC vuông cân tại A. Trên tia đối của tia CA lấy điểm F, trên AB lấy điểm E sao cho BE = CF. Vẽ hình bình hành BEFD.

a) Chứng minh DC vuông góc với BC.

b) Gọi I là giao điểm EF và BC. Chứng minh $AI=\frac{1}{2}DB$.