Cho tứ diện ABCD có AD vuông góc (ABC), ABC là tam giác vuông tại B
Câu hỏi:
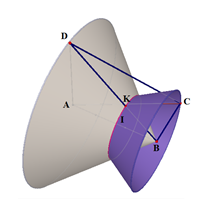
Cho tứ diện ABCD có , ABC là tam giác vuông tại B. Biết . Quay các tam giác ABC và ABD (bao gồm cả điểm bên trong 2 tam giác) xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng:
A.
B.
C.
D.
Trả lời:
Xét mặt phẳng (ABD):
Gọi C’ là điểm ở trong (ABD) sao cho: C’B vuông góc với AB và C’B = BC = a.
Gọi 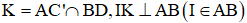
Theo ta-let ta có:
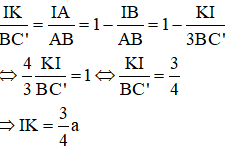
Thể tích của phần chung là
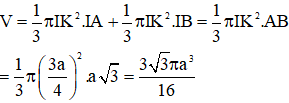
Đáp án cần chọn là: B
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho điểm M, đường tròn trục và các điểm . Chọn mệnh đề sai:
Xem lời giải »
Câu 2:
Cho hình nón tròn xoay có đường cao h = 40 cm, bán kính đáy r = 50 cm. một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 24 cm. Tính diện tích của thiết diện
Xem lời giải »
Câu 3:
Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF
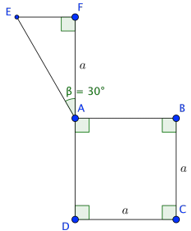
Xem lời giải »
Câu 4:
Cho một khối trụ có chiều cao bằng 8 cm, bán kính đường tròn đáy bằng 6 cm. cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 4cm. Diện tích của thiết diện được tạo thành là:
Xem lời giải »
Câu 5:
Có 4 viên bi hình cầu bán kính bằng 1 cm. Người ta đặt 3 viên bi tiếp xúc nhau và cùng tiếp xúc với mặt bàn. Sau đó đặt 3 viên bi đó lại và đặt 1 viên bi thứ 4 tiếp xúc với cả 3 viên bi trên như hình vẽ bên dưới. Gọi O là điểm thuộc bề mặt của viên bi thứ 4 có khoảng cách đến mặt bàn là lớn nhất. Khoảng cách từ O đến mặt bàn bằng:
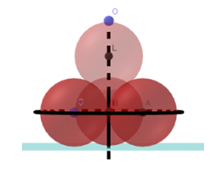
Xem lời giải »

