Góc giữa hai đường thẳng; Góc giữa đường thẳng và mặt phẳng - Toán lớp 12

---

Góc giữa hai đường thẳng; Góc giữa đường thẳng và mặt phẳng

Với Góc giữa hai đường thẳng; Góc giữa đường thẳng và mặt phẳng Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Góc giữa hai đường thẳng; Góc giữa đường thẳng và mặt phẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải

- Cho hai đường thẳng d, d’ có vectơ chỉ phương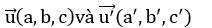

Góc φ giữa hai đường thẳng được tính theo công thức:

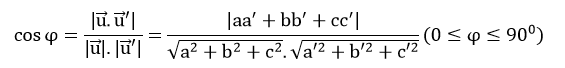
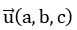
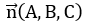
- Cho đường thẳng d có vectơ chỉ phương và mặt phẳng (P) có vectơ pháp tuyến

Góc φ giữa đường thẳng d và mặt phẳng (P) được tính theo công thức:

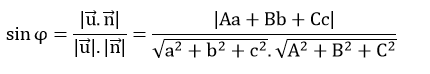
B. Ví dụ minh họa

Ví dụ: 1

Tính cosin góc giữa đường thẳng d với trục Ox biết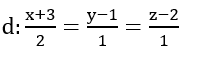

A.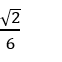

B.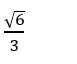

C.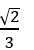

D.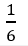

Hướng dẫn giải

Đường thẳng d có vecto chỉ phương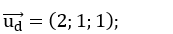

Trục Ox có vecto chỉ phương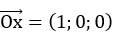

Cosin góc giữa d và Ox là:

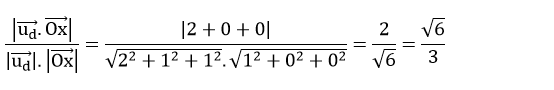
Chọn B.

Ví dụ: 2

Tính góc giữa 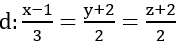và d' là giao tuyến của hai mặt phẳng: (P): x + 2y – z + 1 = 0 và (Q): 2x + 3z – 2 = 0?

A. 30^o

B. 45^o

C. 60^o

D. 90^o

Hướng dẫn giải

Hai mặt phẳng (P)và (Q) có vecto pháp tuyến là: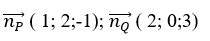

d' là giao tuyến của (P) và (Q) nên vectơ chỉ phương của d’ là

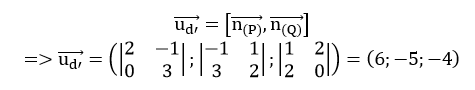
Đường thẳng d có vecto chỉ phương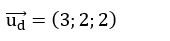

Cosin góc giữa d và d’ là:

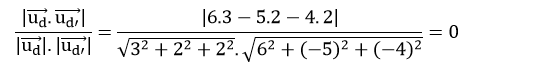
=> góc giữa d và d’ bằng 90^o.

Chọn D.

Ví dụ: 3

Tính sin góc giữa đường thẳng d và mặt phẳng (P) biết 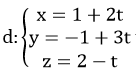và (P): 2x – y + 2z – 1 = 0?

A.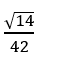

B.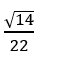

C.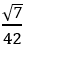

D. Đáp án khác

Hướng dẫn giải

Đường thẳng d có vecto chỉ phương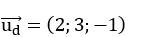

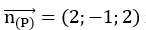
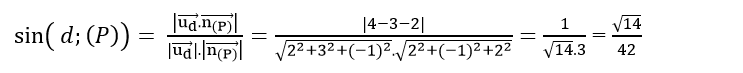
Mặt phẳng (P) có vecto pháp tuyến nên sin góc giữa d và (P) là:

Chọn A.

Ví dụ: 4

Cho bốn điểm A( 1; 0;1) ; B( -1; 2; 1); C( -1; 2; 1) và D( 0; 4; 2). Xác định cosin góc giữa hai đường thẳng AB và CD?

A.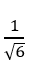

B.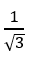

C.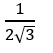

D. Đáp án khác

Hướng dẫn giải

+ Đường thẳng AB có vecto chỉ phương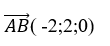

+ Đường thẳng CD có vecto chỉ phương .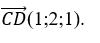

=> Cosin góc giữa hai đường thẳng AB và CD là:

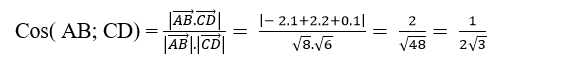
Chọn C.

Ví dụ: 5

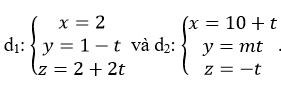
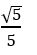
Cho đường thẳng . Xác định m để cosin góc giữa hai đường thẳng đã cho là:

A. m= 2

B. m = - 4

C. m= (- 1)/2

D. m= 1

Hướng dẫn giải

Đường thẳng d₁ có vecto chỉ phương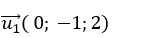

Đường thẳng d₂ có vecto chỉ phương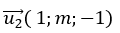

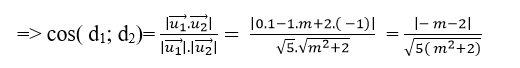
Để cosin góc giữa hai đường thẳng đã cho là:

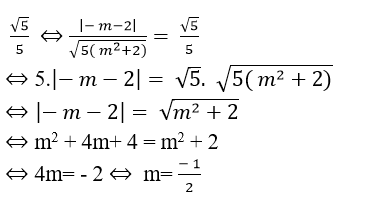
Chọn C.

Ví dụ: 6

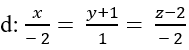
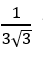
Cho đường thẳng và mặt phẳng (P): x+ my- z+ 100= 0. Xác định m để cosin góc giữa đường thẳng d và mặt phẳng (P) là ?

A. m= ± 1

B.m= ± 2

C. m= 0

D. m= ± 3

Hướng dẫn giải

Đường thẳng d có vecto chỉ phương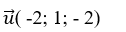

Mặt phẳng (P) có vecto pháp tuyến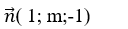

=> Sin góc tạo bởi đường thẳng d và mặt phẳng (P) là:

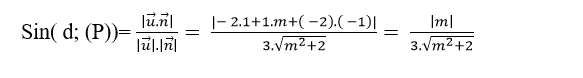
Theo giả thiết ta có:

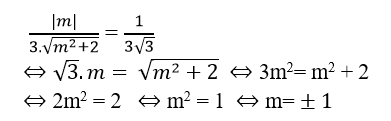
Chọn A.

Ví dụ: 7

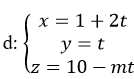
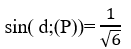
Cho đường thẳng và mặt phẳng (P): 4x- 4y+ 2z- 9= 0. Xác định m để

A. m= 1

B.m= - 1

C. m= - 2

D. m= -1 hoặc m= -7

Hướng dẫn giải

+ Đường thẳng d có vecto chỉ phương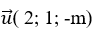

Mặt phẳng (P) có vecto pháp tuyến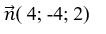

=> Sin góc tạo bởi đường thẳng d và mặt phẳng (P) là:

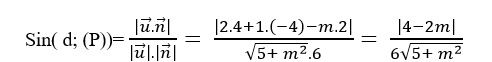
Theo giả thiết ta có: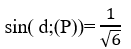

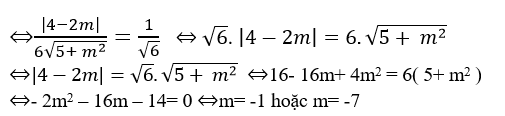
Chọn D.

Ví dụ: 8

Cho đường thẳng 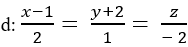; điểm A( 2; 0; 0); B (0; 1; 0) và C( 0;0;- 3).Xác định sin góc giữa đường thẳng d và mặt phẳng (ABC) ?

A.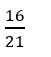

B.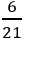

C.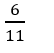

D. Đáp án khác

Hướng dẫn giải

+ Phương trình mặt phẳng (ABC):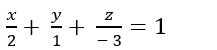

Hay ( ABC): 3x + 6y – 2z – 6= 0

Mặt phẳng (ABC) có vecto pháp tuyến .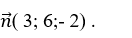

+ Đường thẳng d có vecto chỉ phương .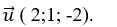

=> Sin góc giữa đường thẳng d và mặt phẳng (P) là:

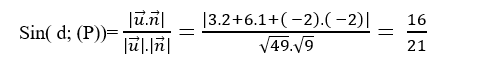
Chọn A.

Ví dụ: 9

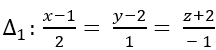
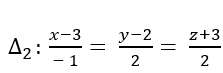
Trong không gian với hệ tọa độ Oxyz; gọi đường thẳng d đi qua A( -1; 0; -1), cắt , sao cho cosin góc giữa d và là nhỏ nhất. Phương trình đường thẳng d là

A.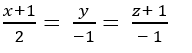

B.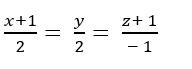

C.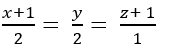

D. Đáp án khác

Hướng dẫn giải

Gọi giao điểm của đường thẳng d và Δ₁ là M( 1+ 2t; 2+ t; -2- t)

Đường thẳng d có vectơ chỉ phương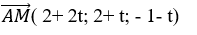

Đường thẳng Δ₂ có vectơ chỉ phương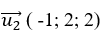

=> cosin góc giữa hai đường thẳng d và Δ₂ là:

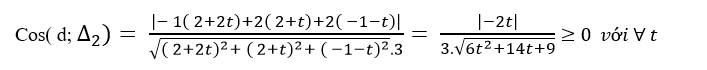
=> cosin góc giữa hai đường thẳng d và Δ₂ là 0 khi t= 0.

Khi đó; M( 1; 2; - 2) và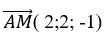

Vậy phương trình đường thẳng d là: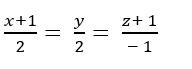

Chọn B.

C. Bài tập vận dụng

Câu 1:

Tính sin của góc tạo bởi đường thẳng 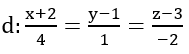và (P):x+y-z+2=0?

A.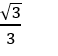

B.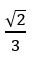

C.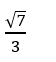

D. Đáp án khác

Lời giải:

Đường thẳng d có vecto chỉ phương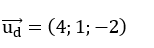

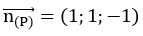
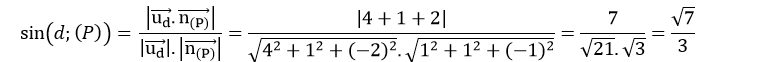
Mặt phẳng (P) có vecto pháp tuyến nên sin góc giữa d và (P) là:

Chọn C.

Câu 2:

Trong không gian với hệ trục toạ độ Oxyz; gọi (P) là mặt phẳng chứa đường thẳng và tạo với trục Oy góc có số đo lớn nhất. Điểm nào sau đây thuộc mặt phẳng (P)?

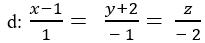
A. ( -3; 0; 4)

B. ( 3; 0; 2)

C. ( -1; -2; -1)

D. ( 1;2;1)

Lời giải:

Gọi 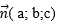là VTPT của (P).

Đường thẳng (d) có vecto chỉ phương .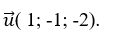

Gọi α là góc tạo bởi (P) và Oy, α lớn nhất khi sinα lớn nhất.

=> n→ vuông góc với u→ nên n→.u→=0

⇔ a- b- 2c= 0 ⇔ a= b+ 2c

=> vecto pháp tuyến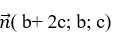

Ta có;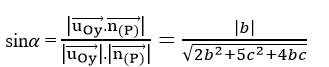

Nếu b= 0 thì sinα= 0

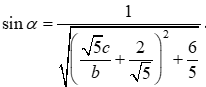
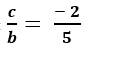
Nếu b ≠ 0 thì . Khi đó, sinα lớn nhất khi:

Chọn b= 5; c= -2 => a= b+ 2c= 1

Vậy phương trình mặt phẳng (P) là x + 5y- 2z + 9= 0. Do đó ta có ( -1; -2; -1) thuộc (P).

Chọn C.

Câu 3:

Trong không gian với hệ tọa độ Oxyz; cho hai đường thẳng . Tính cosin góc giữa hai đường thẳng này?

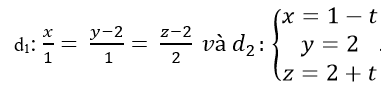
A.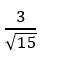

B.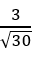

C.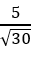

D. Đáp án khác

Lời giải:

+ Đường thẳng d₁ có vecto chỉ phương .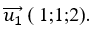

Đường thẳng d₂ có vecto chỉ phương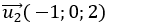

+ Cosin góc giữa hai đường thẳng d₁ và d₂ là:

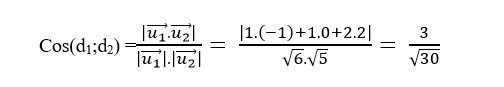
Chọn B.

Câu 4:

Trong không gian với hệ tọa độ Oxyz; cho A(-1; 2; 0); B( 2; 1; 3) và mặt phẳng (P): 2x- y+ z- 2= 0. Sin góc của đường thẳng AB và mặt phẳng (P) là 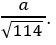. Tính a?

A . 5

B.10

C. 8

D. 7

Lời giải:

+ Đường thẳng AB có vecto chỉ phương là: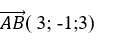

+ Mặt phẳng (P) có vecto pháp tuyến là: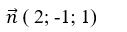

=> Sin góc tạo bởi đường thẳng AB và mặt phẳng (P) là:

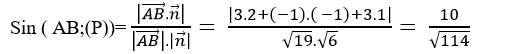
=>a= 10.

Chọn B

Câu 5:

Trong không gian với hệ tọa độ Oxyz; cho đường thẳng 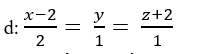mặt phẳng (P): 2x- y- z+ 5= 0 và M( 1; -1; 0). Đường thẳng Δ đi qua điểm M, cắt d và tạo với mặt phẳng (P) một góc thỏa mãn sin (Δ; (P))= 0,5

A.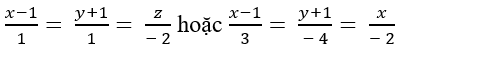

B.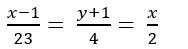

C.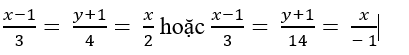

D.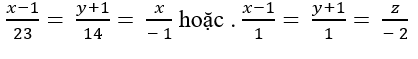

Lời giải:

Gọi giao điểm của d và Δ là N( 2+ 2t; t; - 2+ t)

Đường thẳng Δ có vectơ chỉ phương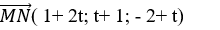

Mặt phẳng (P) có vectơ pháp tuyến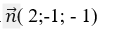

=> sin góc tạo bởi đường thằng Δ và mặt phẳng (P) thỏa mãn:

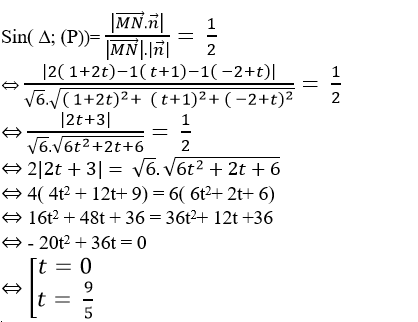
+ Với t= 0 thì N( 2;0; -2 ) và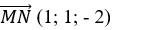

=> Phương trình đường thẳng MN≡Δ: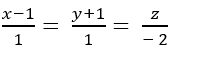

+ Với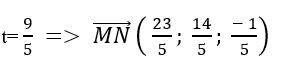

=> Đường thẳng MN nhận vecto ( 23; 14; - 1) làm vecto chỉ phương

=> Phương trình MN: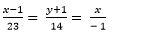

Chọn D.

Câu 6:

Trong không gian với hệ tọa độ Oxyz; gọi d đi qua A( 3; -1; 1) nằm trong mặt phẳng (P): x- y+ z- 5= 0 đồng thời tạo với 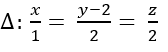một góc 45^o. Phương trình đường thẳng d là

A.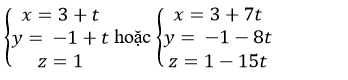

B.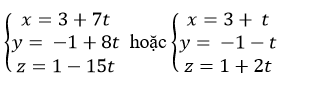

C.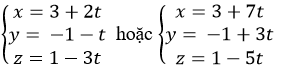

D. Đáp án khác

Lời giải:

+ Đường thăng d có vectơ chỉ phương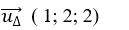

Gọi một vectơ chỉ phương của đường thẳng d là: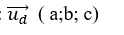

Mặt phẳng (P) có vectơ pháp tuyến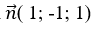

+ Do đường thẳng d nằm trong mặt phẳng (P) nên: u_d→.n→=0

⇔ a- b+ c= 0 ⇔ b= a+ c

+ Do góc giữa đường thẳng ( d) và ( Δ) là 45₀ nên ta có: cos( d;Δ) =cos45^o

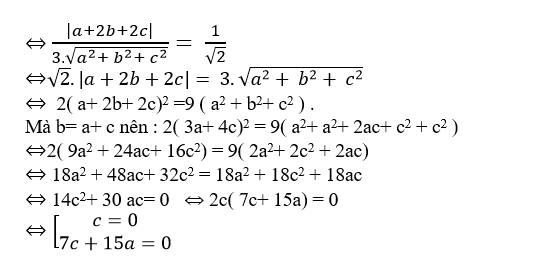
Với c= 0, chọn a= b= 1, phương trình đường thẳng d là: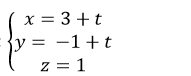

Với 15a+ 7c= 0, chọn a= 7=> c= -15 và b= -8, phương trình đường thẳng d là

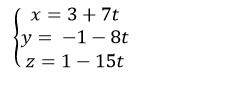
Chọn A

Câu 7:

Trong không gian với hệ tọa độ Oxyz; gọi d đi qua điểm A( 1; -1; 2) , song song với (P): 2x- y- z+ 3= 0 , đồng thời tạo với đường thẳng 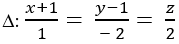một góc α sao cho cosα đạt giá trị nhỏ nhât. Phương trình đường thẳng d là.

A.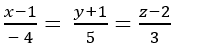

B.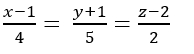

C.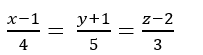

D.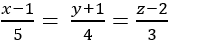

Lời giải:

+ Đường thẳng Δ có vectơ chỉ phương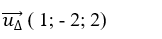

Đường thẳng d có vectơ chỉ phương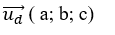

Mặt phẳng (P) có vectơ pháp tuyến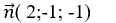

+ Vì d// (P) nên hai vecto u_d→ và n→ vuông góc với nhau.

=> u_d→.n→= 0 ⇔ 2a- b- c= 0 ⇔ c= 2a- b

+ Cosin góc tạo bởi đường thẳng d và Δ là:

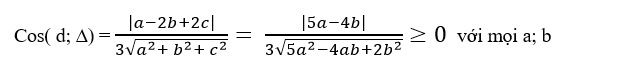
=> cosin góc tạo bởi hai đường thẳng d và Δ đạt giá trị nhỉ nhất là 0 khi 5a- 4b= 0

Chọn a= 4 => b= 5 và c= 3

+ Đường thẳng d đi qua điểm A (1; -1; 2) và nhận vecto 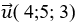làm vecto chỉ phương

=> Phương trình d: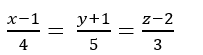

Chọn C.

Câu 8:

Trong không gian Oxyz, cho điểm A( -2; 0; 0), đường thẳng d qua điểm A cắt và tạo với trục Oy góc 45^o. Đường thẳng d có vecto chỉ phương là:

A. ( 2;2; 1) hoặc ( 2;- 2; 1)

B . ( 2; -1;0) hoặc ( 2; 1;0)

C. ( 1;2; 0) hoặc ( - 2; 1;0)

D. ( 2; 2; 0) hoặc ( 2; -2; 0)

Lời giải:

Gọi giao điểm của đường thẳng d và trục Oy là M( 0; m;0)

Trục Oy có vectơ chỉ phương là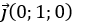

Đường thẳng d có vecto chỉ phương .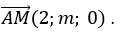

Góc giữa đường thẳng d và trục Oy là 45^o nên ta có:

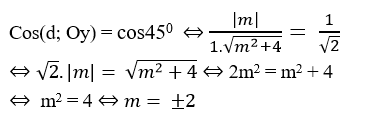
+ Với m= 2 đường thẳng d có vecto chỉ phương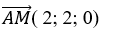

+Với m = -2 đường thẳng d có vecto chỉ phương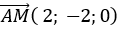

Chọn D.