Vị trí tương đối của đường thẳng và mặt cầu - Toán lớp 12

---

Vị trí tương đối của đường thẳng và mặt cầu

Với Vị trí tương đối của đường thẳng và mặt cầu Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Vị trí tương đối của đường thẳng và mặt cầu từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải

Xét vị trí tương đối của đường thẳng 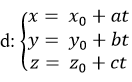và mặt cầu (S) tâm I(a’; b’; c’) bán kính R. Gọi d= d( I; d) thì:

d > R thì d không cắt (S).

d=R thì d tiếp xúc (S). Để tìm tọa độ giao điểm của đường thẳng và mặt cầu ( S) ta làm như sau:

Thay x= x₀+ at; y= y₀ + bt; z= z₀ + ct vào phương trình mặt cầu

=> t= .... => Tọa độ giao điểm.

d < R thì d cắt ( S) tại hai điểm A và B. Để tìm được tọa độ giao điểm ta làm như trên.

* Chú ý: đường thẳng d đí qua A và có vecto chỉ phương u ⃗. Khi đó; khoảng cách từ điểm I đến đường thẳng d là:

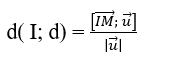
B. Ví dụ minh họa

Ví dụ: 1

Cho mặt cầu (S): x²+ y² + z²- 2x + 4z+ 1= 0 và đường thẳng 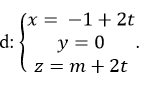. Biết có hai giá trị thực của tham số m để d cắt (S) tại hai điểm phân biệt A; B và các mặt phẳng tiếp diện của ( S) tại A và tại B luôn vuông góc với nhau . Tích của hai giá trị đó bằng

A. 16

B. 12

C.14

D. 10

Hướng dẫn giải

+ Mặt cầu ( S) có tâm I( 1; 0; -2) và bán kính R= 2

Đường thẳng d qua M(- 1; 0; m) và vtcp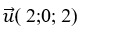

+Đường thẳng d cắt mặt cầu tại hai điểm phân biệt A và B nên IA= IB = R= 2.

Lại có các mặt phẳng tiếp diện của (S) tại A và B vuông góc với nhau nên IA vuông IB.

=> Tam giác IAB vuông cân tại I.

Suy ra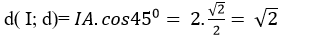

+ Mà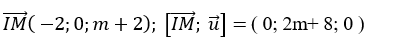

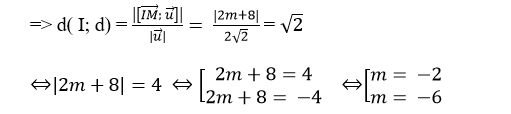
Suy ra m= -2 hoặc m= - 6 và tích cần tìm là ( -2). ( - 6) = 12.

Chọn B.

Ví dụ: 2

Trong không gian Oxyz, cho đường thẳng 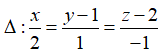và và mặt cầu ( S): x²+ y² + z² – 2x+ 4z + 1= 0. Số điểm chung của Δ và ( S) là

A.0

B.1

C.2.

D. 3

Hướng dẫn giải

Đường thẳng đi qua M( 0; 1; 2) và có VTCP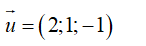

Mặt cầu (S) có tâm I (1; 0; -2) và bán kính R= 2.

Ta có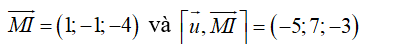

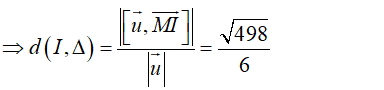
Vì d(I,Δ)>R nên không cắt mặt cầu ( S) .

Chọn A.

Ví dụ: 3

Trong không gian Oxyz, cho đường thẳng 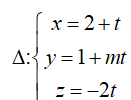và mặt cầu ( S): (x-1)²+ ( y+ 3)² + ( z- 2)²= 1. Giá trị của m để đường thẳng không cắt mặt cầu ( S) là:

A.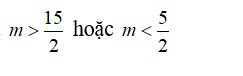

B.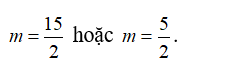

C.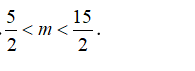

D.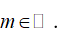

Hướng dẫn giải

Giao điểm nếu có của đường thẳng Δ và mặt cầu (S) là nghiệm hệ phương trình :

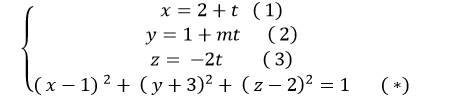
Thay (1); ( 2) và (3) vào ( *) ta được:

(2+t+1)²+(1+mt+3)²+(-2t-2)²=1

⇔ ( t+ 1)² + ( mt+ 4)²+ ( 2t+ 2)² = 1

⇔ t² + 2t+ 1+ m²t² + 8mt+ 16 + 4t2 + 8t+ 4- 1= 0

⇔ (m² + 5)t² + 2( 5+ 4m)t+ 20 = 0 ( **)

Để không cắt mặt cầu ( S) thì (**) vô nghiệm, hay (**) có Δ’<0

⇔ ( 5+ 4m)² – 20( m² + 5) < 0

⇔ 25+ 40m+ 16m² – 20m² – 100< 0

⇔ - 4m² + 40m – 75 < 0

.

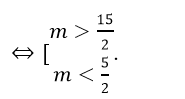
Chọn A.

Ví dụ: 4

Trong không gian Oxyz, cho mặt cầu ( S): ( x-1)₂ + ( y+3)₂ + ( z- 2)₂ =1và đường thằng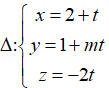 . Giá trị của m để đường thẳng Δ tiếp xúc mặt cầu (S) là:

A.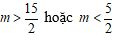

B. .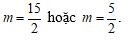

C.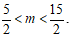

D.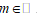

Hướng dẫn giải

Giao điểm nếu có của đường thẳng Δ và mặt cầu (S) là nghiệm hệ phương trình :

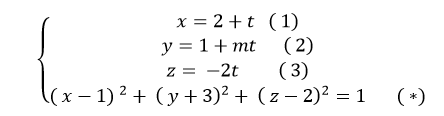
Thay (1); ( 2) và (3) vào ( *) ta được:

(2+t-1)₂ + (1 + mt + 3)₂ + (-2t-2)₂=1

⇔ ( t+ 1)₂ + ( mt+ 4)₂+ ( 2t+ 2)₂ = 1

⇔ t₂ + 2t+ 1+ m₂t₂ + 8mt+ 16 + 4t₂ + 8t+ 4- 1= 0

⇔ (m₂ + 5)t₂ + 2( 5+ 4m)t+ 20 = 0 ( **)

Để Δ tiếp xúc mặt cầu ( S) thì (**) có nghiệm kép nên:

.

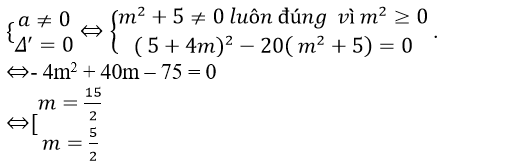
Chọn B.

Ví dụ: 5

Trong không gian Oxyz, cho mặt cầu ( S): x² +( y+1)² + (z- 1)² = 4 và đường thẳng 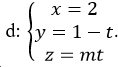. Giá trị của m để đường thẳng d cắt mặt cầu ( S) tại hai điểm phân biệt là:

A. m < 2 hoặc m > 5.

B. m > - 2 hoặc m - 5

C. m= 2 hoặc m = - 5

D. Không có giá trị nào của m thỏa mãn.

Hướng dẫn giải

Giao điểm nếu có của đường thẳng d và mặt cầu ( S) là nghiệm hệ phương trình :

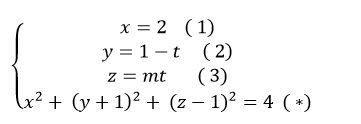
Thay (1); (2) ; (3) vào (*) ta được:

2² + ( 1- t+ 1)² + ( mt- 1)² =4

⇔ 4+ 4 – 4t+ t²+ t + m²t² - 2mt+ 1- 4= 0

⇔ ( m²+ 1)t² – ( 3+ 2m)t+ 5=0 ( **)

Để đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt khi và chỉ khi phương trình (**) có hai nghiệm phân biệt

⇔ Δ >0 ⇔ ( 3+ 2m)² – 4. 5.( m² +1) > 0

⇔ 9+ 12m + 4m² – 20m² – 20> 0

⇔ - 16m² + 12m- 11> 0 ( vô lí - vì – 16m² + 12m- 11 < 0 với mọi m)

Chọn D.

Ví dụ: 6

Trong không gian Oxyz, cho đường thẳng 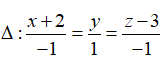và và mặt cầu (S): x² + y² + z² – 2x – 4y+ 6z – 67= 0. Số điểm chung của Δ và( S) là:

A.3.

B.0.

C.1

D. 2

Hướng dẫn giải

Đường thẳng đi qua M(-2; 0; 3) và có VTCP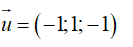

Mặt cầu ( S) có tâm I( 1; 2; - 3) và bán kính R= 9.

Ta có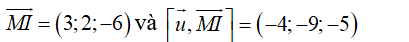

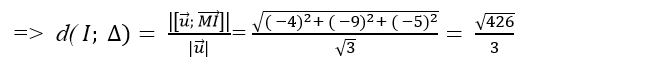
Vì d( I;Δ) < R nên cắt mặt cầu ( S) tại hai điểm phân biệt.

Chọn D.

Ví dụ: 7

Trong không gian với hệ tọa độ Oxyz; cho đường thẳng 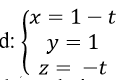và mặt cầu ( S): ( x-1)² + ( y+ m)²+ z² = 1. Tìm điều kiện của m để đường thẳng d và mặt cầu ( S) có điểm chung?

A. -1≤ m ≤ 0 .

B. m > - 2 hoặc m < - 3

C. m > 1 hoặc m < 0

D. Đáp án khác

Hướng dẫn giải

Giao điểm nếu có của đường thẳng d và mặt cầu ( S) là nghiệm hệ phương trình :

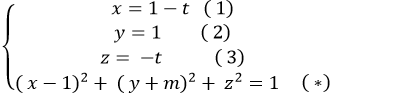
Thay (1); ( 2) và ( 3)vào ( *) ta được:

( 1- t – 1)² + ( 1+ m)² + t² = 1

⇔ t²+ 1+ 2m+ m² + t² – 1= 0

⇔ 2t² + 2m + m² = 0

⇔ t² = - m- m² ( **)

Để đường thẳng d và mặt cầu ( S) có điểm chung khi và chỉ khi phương trình ( **) có nghiệm nên: - m – m² ≥ 0 ⇔ - 1 ≤ m ≤ 0 .

Chọn A.

C. Bài tập vận dụng

Câu 1:

Cho mặt cầu (S): x²+ y² + z²+ 2x – 4y+ 4z= 0 và đường thẳng 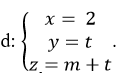. Có bao nhiêu giá trị nguyên của m để đường thẳng d cắt mặt cầu ( S) tại hai điểm phân biệt

A.2

B. 3

C.4

D. Vô số

Lời giải:

+ Mặt cầu ( S) có tâm I(- 1; 2; - 2) và bán kính R= 3

Đường thẳng d qua M( 2; 0; m) và vtcp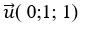

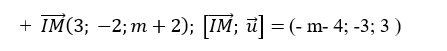
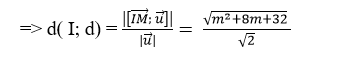
+ Để đường thẳng d cắt mặt cầu ( S) tại hai điểm phân biệt khi và chỉ khi:

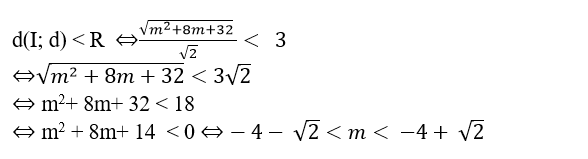
Mà m nguyên nên m= - 5; m= - 4 hoặc m = -3

Chọn B.

Câu 2:

Trong không gian Oxyz, cho đường thẳng 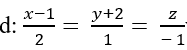và và mặt cầu ( S): x²+ y² + z² – 2x- 2z + 1= 0. Số điểm chung của và ( S) là

A.0

B.1

C.2.

D. 3

Lời giải:

Đường thẳng d đi qua M( 1; -2; 0) và có VTCP .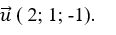

Mặt cầu (S) có tâm I (1; 1; 0) và bán kính R= 1.

Ta có:

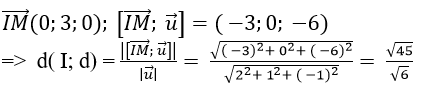
Vì d( I; d)> 1 nên d không cắt mặt cầu ( S) .

Chọn A.

Câu 3:

Trong không gian Oxyz, cho đường thẳng 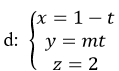và mặt cầu ( S): x²+ ( y- 2)² + ( z+ 2)²= 1. Giá trị của m để đường thẳng d không cắt mặt cầu ( S) là

:

A.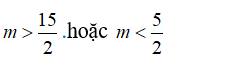

B.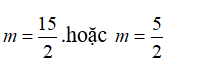

C.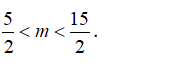

D.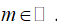

Lời giải:

Giao điểm nếu có của đường thẳng d và mặt cầu (S) là nghiệm hệ phương trình :

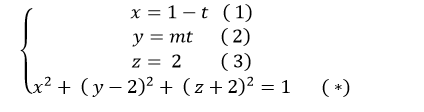
Thay (1); ( 2) và (3) vào ( *) ta được: x

( 1- t)² + (mt- 2)² + ( 2+ 2)² = 1

⇔ 1- 2t + t² + m²t² – 4mt + 4 + 16 – 1= 0

⇔ ( m²+1) t² - 2( 1+ 2m)t + 20= 0 ( **)

Để d không cắt mặt cầu ( S) thì (**) vô nghiệm, hay (**) có Δ’<0

⇔ (1+ 2m)² – 20( m² + 1) < 0

⇔ 1+ 4m+ 4m² – 20m² – 20< 0

⇔ - 16m² + 4m – 19< 0 luông đúng với mọi m ( vì hệ số a= -16 < 0 và Δ’<0 với mọi m)

Chọn D.

Câu 4:

Trong không gian Oxyz, cho mặt cầu ( S): x² + ( y+3)² + z² = 4 và đường thẳng 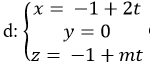Giá trị của m để đường thẳng d tiếp xúc mặt cầu (S) là:

A. m < 1 hoặc m> 3

B. m= 1 hoặc m= - 3.

C.không có giá trị nào của m thỏa mãn

D.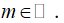

Lời giải:

Giao điểm nếu có của đường thẳng d và mặt cầu (S) là nghiệm hệ phương trình :

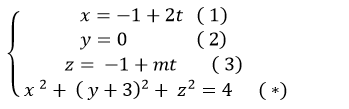
Thay (1); ( 2) và (3) vào ( *) ta được:

( - 1+ 2t)² + (0+ 3)² + ( - 1+ mt)² = 4

⇔ 1- 4t + 4t²+ 9+ 1- 2mt + m²t² – 4= 0

⇔ ( m²+ 4)t² – 2( 2+ m) t+ 7= 0

Để d tiếp xúc mặt cầu ( S) thì (**) có nghiệm kép nên:

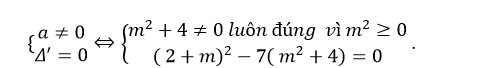
⇔ 4+ 4m+ m² - 7m² – 28 = 0

⇔ - 6m²+ 4m- 24= 0 ( phương trình vô nghiệm vì Δ= 4²-4.( -6).( -24)<0

Vậy không có giá trị nào của m để d tiếp xúc với mặt cầu

Chọn C.

Câu 5:

Trong không gian Oxyz, cho mặt cầu ( S): (x- 2)² +( y-1)² + (z- 1)² =1 và đường thẳng 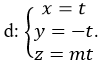. Giá trị của m để đường thẳng d cắt mặt cầu ( S) tại hai điểm phân biệt là:

A. m < 2 hoặc m > 5.

B. m > - 2 hoặc m - 5

C. m= 2 hoặc m = - 5

D. Không có giá trị nào của m thỏa mãn.

Lời giải:

Giao điểm nếu có của đường thẳng d và mặt cầu ( S) là nghiệm hệ phương trình :

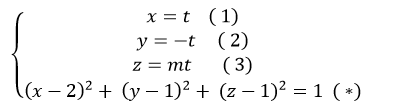
Thay (1); (2) ; (3) vào (*) ta được:

( t- 2)² + ( - t- 1)² + (mt- 1)² = 1

⇔ t² – 4t + 4 + t² + 2t +1+ m² t² - 2mt + 1- 1= 0

⇔ ( m² + 2)t² – 2( 1+ m)t+ 5= 0

Để đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt khi và chỉ khi phương trình (**) có hai nghiệm phân biệt

⇔ Δ' >0 ⇔ (1+m)2 – 5( m2+ 2) > 0

⇔ 1+ 2m+ m² - 5m² – 10> 0

⇔ - 4m² + 2m- 9 > 0 vô lí

vì hệ số a= -4 < 0 và Δ_m= 4- 4( -4). (-9)< 0 nên - 4m² + 2m- 9< 0 với mọi m.

Chọn D

Câu 6:

Trong không gian Oxyz, cho đường thẳng 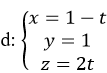và và mặt cầu (S): x²+ y² + z² – 2x + 4y - 2z – 3= 0. Số điểm chung của Δ và( S) là:

A. 3.

B.0.

C.1

D. 2

Lời giải:

Đường thẳng d đi qua M(1; 1;0) và có VTCP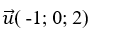

Mặt cầu ( S) có tâm I(1; -2; 1) và bán kính R= 3.

Ta có

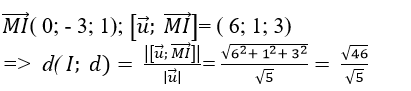
Vì d( I;Δ)> R nên d không cắt mặt cầu ( S).

Chọn B.

Câu 7:

Trong không gian với hệ tọa độ Oxyz; cho đường thẳng 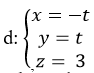và mặt cầu ( S): ( x+2)² + ( y- m)²+ (z-1)² = 4. Tìm điều kiện của m để đường thẳng d và mặt cầu ( S) có điểm chung?

A. -1≤m≤0 .

B. m= 2

C. m > 2

D. Đáp án khác

Lời giải:

Giao điểm nếu có của đường thẳng d và mặt cầu ( S) là nghiệm hệ phương trình :

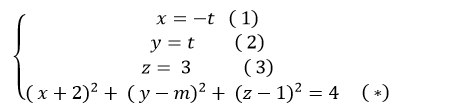
Thay (1); ( 2) và ( 3)vào ( *) ta được:

( -t+2)²+ ( t- m)² + ( 3-1)² = 4

⇔ t² – 4t + 4 + t² – 2mt + m² + 4- 4= 0

⇔ 2t² – 2( 2+ m)t+ 4+ m² = 0 ( **)

Để đường thẳng d và mặt cầu ( S) có điểm chung khi và chỉ khi phương trình ( **) có nghiệm nên: Δ'≥0 ⇔ ( 2+ m)² – 2( 4 +m²)≥0

⇔ 4+ 4m+ m² – 8 – 2m² ≥0 ⇔ - m²+ 4m- 4≥0

⇔ - (m-2)²≥0 ⇔ m= 2

Chọn B.