Gọi (H) là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy
Câu hỏi:
Gọi (H) là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy để 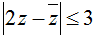 với số phức z có phần thực không âm. Tính diện tích hình (H).
với số phức z có phần thực không âm. Tính diện tích hình (H).
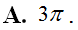
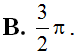
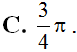
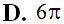
Trả lời:
Chọn A.
+ Giả sử z = a + bi, khi đó 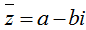 , giả thiết của bài toán là
, giả thiết của bài toán là
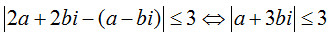
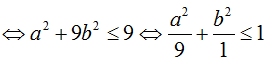
+ Vậy tập hợp các điểm biểu diễn cho số phức z là điểm M(a; b) thuộc miền trong của elip 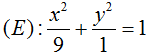 (kể cả các điểm trên biên).
(kể cả các điểm trên biên).
+ Bán trục lớn của ( E) là a = 3, bán trục bé của ( E) là b = 1 nên diện tích cần tính của miền ( H) là S = πab = 3π.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hai số phức z1; z2 khác 0 thỏa mãn .Gọi A; B lần lượt là các điểm biểu diễn cho số phức z1; z2. Khi đó tam giác OAB là:
Xem lời giải »
Câu 2:
Cho số phức z thỏa mãn . Giá trị của |z| là ?
Xem lời giải »
Câu 4:
Số nghiệm của phương trình với ẩn số phức z: 4z2 + 8|z|2 - 3 = 0 là:
Xem lời giải »
Câu 5:
Có số phức z có phần ảo bằng 164 và n ∈ R* thỏa mãn: 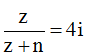 . Tìm n?
. Tìm n?
Xem lời giải »
Câu 6:
Tìm số phức z thỏa mãn hai điều kiện:| z + 1 - 2i| = | + 3 + 4i| và là một số thuần ảo.
Xem lời giải »
Câu 7:
Trong các số phức z thỏa mãn điều kiện | z - 2 + 3i | = . Số phức z có mođun nhỏ nhất có phần thực gần với giá trị nào nhất?
Xem lời giải »
Câu 8:
Tìm số phức z thỏa mãn (z - 1)( + 2i) là số thực và |z| đạt giá trị nhỏ nhất.
Xem lời giải »
![]() với số phức z có phần thực không âm. Tính diện tích hình (H).
với số phức z có phần thực không âm. Tính diện tích hình (H). , giả thiết của bài toán là
(kể cả các điểm trên biên).

