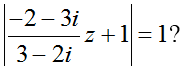Trong các số phức z thỏa mãn điều kiện | z - 2 + 3i | =3/2
Câu hỏi:
Trong các số phức z thỏa mãn điều kiện | z - 2 + 3i | = . Số phức z có mođun nhỏ nhất có phần thực gần với giá trị nào nhất?
A. 1,17
B. 1,16
C. 1,15
D. 1,14
Trả lời:
Chọn A.
Đặt z = x+ yi.
Khi đó
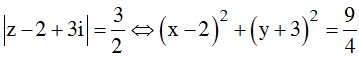
Các điểm M biểu diễn số phức z thỏa mãn hệ thức đã cho nằm trên đường tròn tâm I(2;-3) và bán kính R = 3/2.
Ta có: min|z| khi và chỉ khi M nằm trên đường tròn và gần O nhất.
Đó là điểm M1( là giao điểm của tia IO với đường tròn) (Bạn đọc tự vẽ hình).
Ta có: 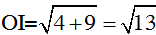 . Kẻ
. Kẻ 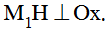
Theo định lý Talet ta có:
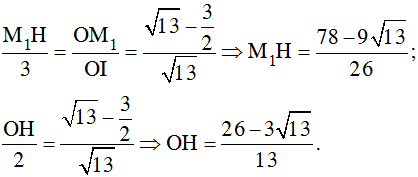
Vậy 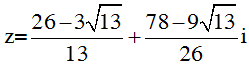
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hai số phức z1; z2 khác 0 thỏa mãn .Gọi A; B lần lượt là các điểm biểu diễn cho số phức z1; z2. Khi đó tam giác OAB là:
Xem lời giải »
Câu 2:
Cho số phức z thỏa mãn . Giá trị của |z| là ?
Xem lời giải »
Câu 4:
Số nghiệm của phương trình với ẩn số phức z: 4z2 + 8|z|2 - 3 = 0 là:
Xem lời giải »
Câu 5:
Tìm số phức z thỏa mãn (z - 1)( + 2i) là số thực và |z| đạt giá trị nhỏ nhất.
Xem lời giải »
Câu 6:
Trong các số phức z thỏa mãn |z - 3i| + | i + 3| =10 , tìm số phức z có mô-đun nhỏ nhất.
Xem lời giải »
Câu 7:
Trong các số phức z thỏa mãn | z - 2 + i | = | + 1 -4i | , tìm số phức có mô-đun nhỏ nhất.
Xem lời giải »
. Kẻ