Hàm số y = x+ căn bậc hai của 4 - x^2 với x thuộc [-2; 1/2] đạt giá trị lớn nhất tại x bằng
Câu hỏi:
Hàm số với đạt giá trị lớn nhất tại x bằng
A. 1
B.
C. -2
D. -1
Trả lời:
Chọn B
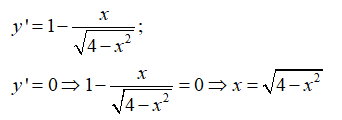
Vậy hàm số đã cho đạt giá trị lớn nhất khi x =
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm m để có hai điểm cực trị tại thỏa mãn
Xem lời giải »
Câu 2:
Tìm m để hàm số luôn đồng biến trên từng khoảng xác định của nó
Xem lời giải »
Câu 3:
Tìm m để phương trình có 6 nghiệm phân biệt
Xem lời giải »
Câu 4:
Tìm m để hàm số có cực đại, cực tiểu nằm về hai phía so với trục tung
Xem lời giải »
Câu 5:
Tìm m để đồ thị hàm số có ba cực trị tạo thành tam giác vuông cân
Xem lời giải »
Câu 6:
Tìm m để đồ thị hàm số có ba cực trị tạo thành tam giác vuông cân
Xem lời giải »
