Lý thuyết về mặt tròn xoay hay, chi tiết nhất - Toán lớp 12

Lý thuyết về mặt tròn xoay hay, chi tiết nhất

Tài liệu Lý thuyết về mặt tròn xoay hay, chi tiết nhất Toán lớp 12 sẽ tóm tắt kiến thức trọng tâm về mặt tròn xoay từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 12.

1. Sự tạo thành mặt tròn xoay

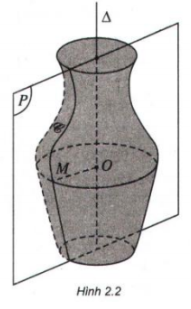
Trong không gian cho mặt phẳng (P) chứa đường thẳng Δ và một đường C. Khi quay mặt phẳng (P) quanh Δ một góc 360º thì mỗi điểm M trên đường C vạch ra một đường tròn có tâm O thuộc Δ và nằm trên mặt phẳng vuông góc với Δ. Như vậy, khi quay mặt phẳng (P) quanh đường thẳng Δ thì đường C sẽ tạo nên một hình được gọi là mặt tròn xoay.

Đường C được gọi là đường sinh của mặt tròn xoay đó. Đường thẳng Δ được gọi là trục của mặt tròn xoay.

2. Tính chất của mặt tròn xoay

- Nếu cắt mặt tròn xoay bởi một mặt phẳng vuông góc với trục Δ ta được phần giao là đường tròn có tâm thuộc Δ.

- Mỗi điểm M trên mặt tròn xoay đều nằm trên một đường tròn thuộc mặt tròn xoay và đường tròn này có tâm thuộc trục Δ.

3. Ví dụ minh họa

Ví dụ 1 Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy SC = a√6 . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:

Hướng dẫn giải:

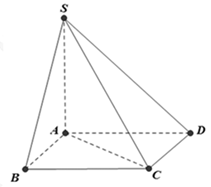
+ Do ABCD là hình vuông cạnh a nên AC = a√2

+ Xét tam giác SAC có:
SA = 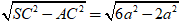= 2a

+ Hình nón tròn xoay được tạo thành có bán kính đường tròn đáy r = AC = a√2 ; đường cao SA = 2a. Do đó, thể tích hình nón là:

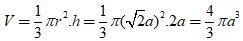
Chọn A.

Ví dụ 2 Trong không gian, cho tam giác ABC cân tại A, AB = a√7 ; BC = 4a. Gọi H là trung điểm của BC. Tính thể tích V của hình nón nhận được khi quay tam giác ABC xung quanh trục AH.

Hướng dẫn giải:

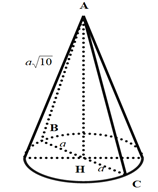
Do tam giác ABC là tam giác cân tại A có AH là đường trung tuyến nên AH ⊥ BC

Khi quay tam giác ABC xung quanh trục AH ta được hình nón có:

+ Đường sinh l = AB = a√7

+ Bán kính đáy r = 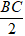= 2a

Suy ra đường cao của hình nón là:

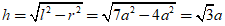
+ Thể tích của hình nón tạo thành là:

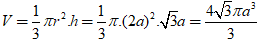
Chọn A.

Ví dụ 3 Cho một hình cầu bán kính 5, cắt hình cầu này bằng một mặt phẳng sao cho thiết diện tạo thành là một đường kính 4. Tính thể tích của khối nón có đáy là thiết diện vừa tạo và đỉnh là tâm hình cầu đã cho. ( kết quả làm tròn tới hàng phần trăm).

A.18,18    B. 19,19    C. 19,2.    D. 17,16

Hướng dẫn giải:

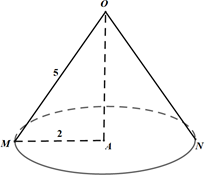
Gọi thiết diện là đường tròn tâm A, đường kính d= 4 ⇒ bán kính r = 2. Gọi MN là một đường kính của đường tròn (A).

Gọi O là tâm của mặt cầu đã cho.

Hình nón có đáy là thiết diện là hình tròn tâm A và đỉnh là O có:

• Bán kính đường tròn đáy là: r = 2.

• Đường sinh là OM = 5 ( = bán kính của hình cầu đã cho)

• Chiều cao:

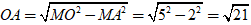
Diện tích đường tròn đáy là: S = πr² = 4π

Thể tích khối nón cần tính là:

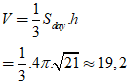
Chọn C