Cách xác định Thiết diện của hình nón cực hay - Toán lớp 12
Cách xác định Thiết diện của hình nón cực hay
Với Cách xác định Thiết diện của hình nón cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập xác định Thiết diện của hình nón từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ
- Nếu cắt mặt nón tròn xoay bởi mặt phẳng đi qua đỉnh thì có các trường hợp sau xảy ra:
+ Mặt phẳng cắt mặt nón theo 2 đường sinh thì thiết diện là tam giác cân.
+ Mặt phẳng tiếp xúc với mặt nón theo một đường sinh, trong trường hợp này, người ta gọi đó là mặt phẳng tiếp diện của mặt nón.
- Nếu cắt mặt nón tròn xoay bởi mặt phẳng không đi qua đỉnh thì có các trường hợp sau xảy ra:
+ Nếu mặt phẳng cắt vuông góc với trục hình nón thì giao tuyến là một đường tròn.
+ Nếu mặt phẳng cắt song song với 2 đường sinh hình nón thì giao tuyến là 2 nhánh của 1 hypebol.
+ Nếu mặt phẳng cắt song song với 1 đường sinh hình nón thì giao tuyến là 1 đường parabol.
Ví dụ minh họa
Bài 1: Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh 2a. Tính diện tích xung quanh của hình nón.
Hướng dẫn:
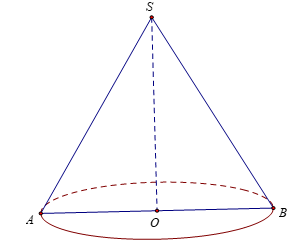
Cắt hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là tam giác SAB, ∆SAB đều cạnh 2a.
Sxq = πRl = π.a.2a = 2πa2
Bài 2: Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng a√2. Tính thể tích khối nón.
Hướng dẫn:
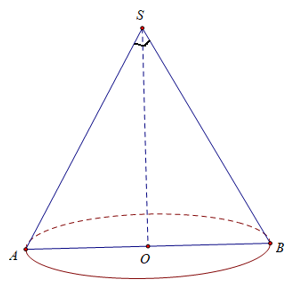
Thiết diện thu được khi cắt hình nón bằng mặt phẳng đi qua trục là tam giác SAB
⇒∆SAB vuông cân tại S, có AB = a√2
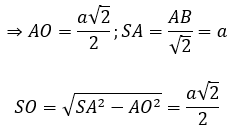
Thể tích khối nón là:
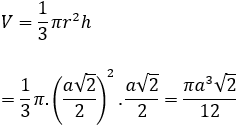
Bài 3: Một hình nón có đường sinh bằng 3cm và góc ở đỉnh bằng 90°. Cắt hình nón bởi mặt phẳng (α) đi qua đỉnh sao cho góc giữa (α) và mặt đáy bằng 60°. Tính diện tích thiết diện
Hướng dẫn:
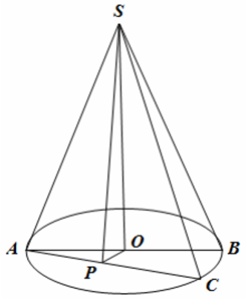
Dựng hình như hình bên với (α) là (SAC).
+ ∆SAB vuông cân tại S
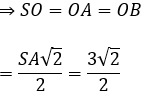
+ Kẻ OP ⊥ AC
Ta có: OP ⊥ AC; SO ⊥ AC ⇒ SP ⊥ AC
Khi đó, góc giữa (SAC) và đáy là góc giữa SP và OP
⇒ ∠(SPO) = 60º
Xét ∆SPO vuông tại O có:
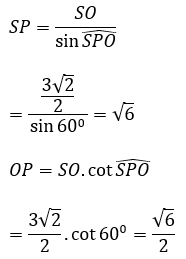
Ta có:
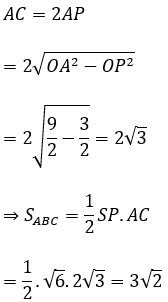
Bài 4: Khối nón (N) có chiều cao bằng 3a. Thiết diện song song và cách mặt đáy một đoạn bằng a, có diện tích bằng 64π/9 . a2. Khi đó, thể tích của khối nón (N) bằng bao nhiêu?
Hướng dẫn:
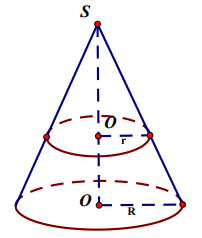
Thiết diện thu được khi cắt hình nón bởi mặt phẳng song song với đáy là hình tròn tâm O’ có bán kính r
Diện tích của thiết diện:
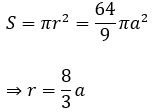
Theo giả thiết, SO = 3a, OO’ = a ⇒ SO’ = 2a
Ta có:
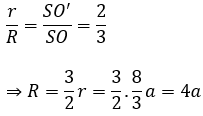
Vậy thể tích khối chóp là:
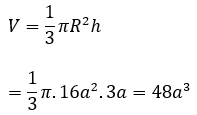
Bài 5: Tính diện tích toàn phần của hình nón có khoảng cách từ tâm của đáy đến đường sinh bằng √3 và thiết diện qua trục là tam giác đều.
Hướng dẫn:
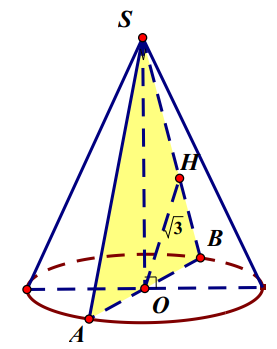
Thiết diện là ∆SAB, đặt AB = a.
Xét ∆SOB vuông tại O, OH là đường cao có:
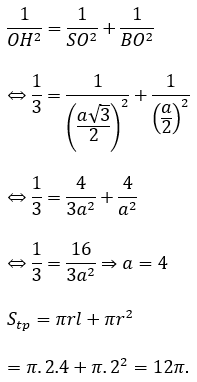
B. Bài tập vận dụng
Bài 1: Cắt hình nón (N) bằng một mặt phẳng đi qua trục của hình nón được thiết diện là một tam giác vuông cân có diện tích bằng 3a2. Diện tích xung quanh của (N) là:
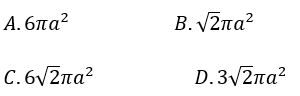
Lời giải:
Đáp án : D
Giải thích :
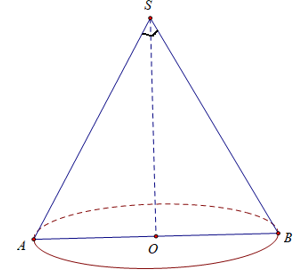
∆SAB vuông cân tại S
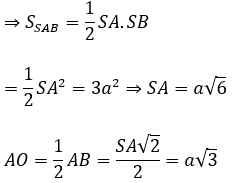
Diện tích xung quanh của hình nón là:
Sxq = πrl = π.AO.SA = π.a√6.a√3 = 3πa2 √2
Bài 2: Thiết diện qua trục của một hình nón là một tam giác vuông cân có diện tích 50 (cm2). Thể tích khối nón là:
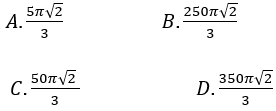
Lời giải:
Đáp án : B
Giải thích :
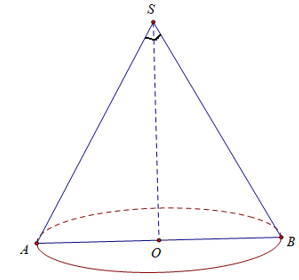
∆SAB vuông cân tại S
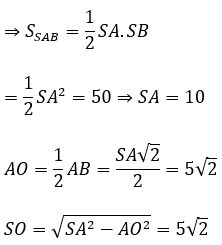
Thể tích của khối nón là:
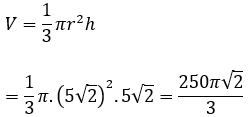
Bài 3: Thiết diện qua trục của hình nón là tam giác đều cạnh là 6cm. Thiết diện qua hai đường sinh và hai đường sinh tạo thành góc 30º, thì diện tích của nó tính bằng cm2 là:

Lời giải:
Đáp án : A
Giải thích :
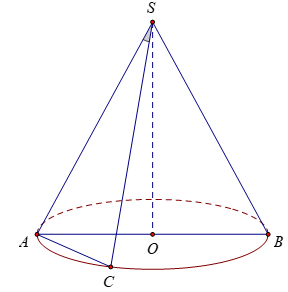
∆SAB đều có cạnh bằng 6 ⇒ SA=6
∆SAC cân tại S nên SA = SC = 6
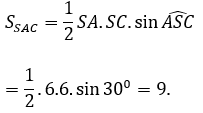
Bài 4: Cho hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh huyền 2a. Thể tích của khối nón bằng

Lời giải:
Đáp án : A
Giải thích :
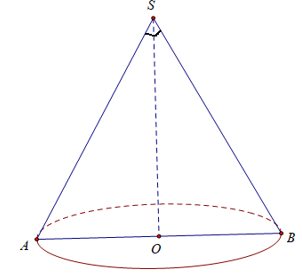
∆SAB vuông cân tại S có AB = 2a
∆SAO vuông cân tại O có AO=SO=AB/2=a
Thể tích của khối nón là:
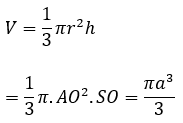
Bài 5: Cho hình nón có đáy là đường tròn đường kính 10, chiều cao 15. Mặt phẳng vuông góc với trục cắt hình nón theo giao tuyến là một đường tròn. Thể tích của khối nón có đường cao bằng 6 là:
Lời giải:
Đáp án : B
Giải thích :
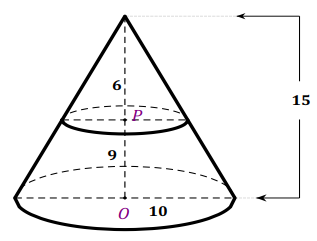
Ta có:
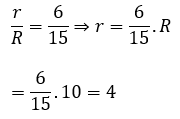
Vậy thể tích khối chóp có đường cao bằng 6 là:
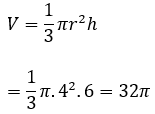
Bài 6: Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh góc vuông bằng a. Một thiết diện qua đỉnh tạo với đáy một góc 60º. Diện tích của thiết diện này bằng:
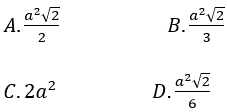
Lời giải:
Đáp án : B
Giải thích :
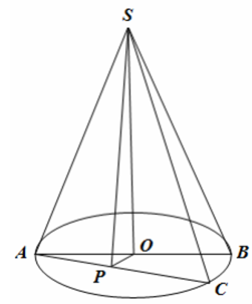
Thiết diện qua đỉnh tạo với đáy một góc 60º là ∆SAC
+ ∆SAB vuông cân tại S, có SA = a
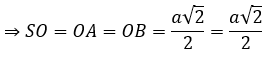
+ Kẻ OP ⊥ AC
Ta có: OP ⊥ AC;SO ⊥ AC ⇒ SP ⊥ AC
Khi đó, góc giữa (SAC) và đáy là góc giữa SP và OP
⇒ ∠(SPO) = 60º
Xét ∆SPO vuông tại O có:
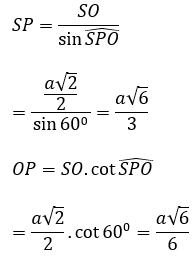
Ta có:
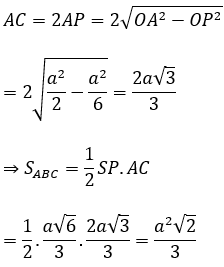
Bài 7: Hình nón có đường cao 20 cm, bán kính đáy 25 cm. Một mặt phẳng (P) qua đỉnh của hình nón và có khoảng cách đến tâm là 12cm. Diện tích thiết diện tạo bởi (P) và hình nón là
Lời giải:
Đáp án : B
Giải thích :
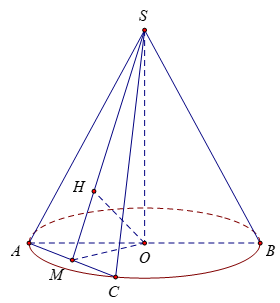
Gọi M là trung điểm của AC. Kẻ OH ⊥ SM
∆SAC cân tại S nên SM ⊥ AC
Lại có SO ⊥ AC
⇒ (SMO) ⊥ AC ⇒ OH ⊥ AC
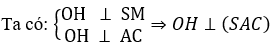
Do đó, khoảng cách từ tâm đến (P) là độ dài đoạn OH ⇒ OH=12
Xét tam giác SMO vuông tại O, OH là đường cao có:
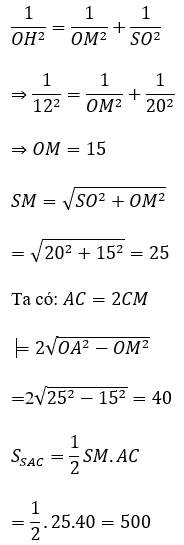
Bài 8: Một hình nón đỉnh S có tâm mặt đáy là O. Cắt hình nón bởi một mặt phẳng (P) đi qua S được thiết diện là một tam giác đều cạnh A. Biết góc giữa (P) và mặt đáy bằng 45º. Thể tích khối nón được tính theo a là:

Lời giải:
Đáp án : D
Giải thích :
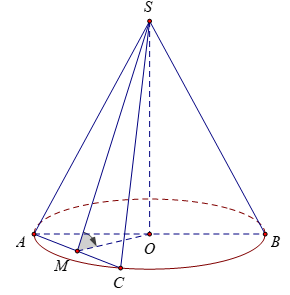
Mặt phẳng (P) cắt hình nón theo thiết diện là tam giác SAC
Gọi M là trung điểm của AC. Kẻ OH ⊥ SM
∆SAC cân tại S nên SM ⊥ AC
Lại có SO ⊥ AC
⇒ (SMO) ⊥ AC ⇒ OM ⊥ AC
Khi đó, góc giữa (P) và mặt đáy là góc giữa SM và OM
⇒ ∠(SMO) = 45º
Theo giả thiết ∆SAC đều cạnh a nên SA=a; SM=(a√3)/2
Xét tam giác SMO vuông tại O có ∠(SMO) = 45º
⇒ ∆SMO vuông cân tại O
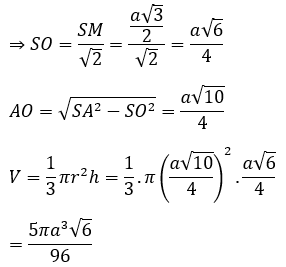
Bài 9: Cho hình nón có độ dài đường sinh là l=4 cm, bán kính đường tròn đáy là r=2 cm. Thiết diện qua trục của hình nón là hình gì?

Lời giải:
Đáp án : C
Giải thích :
Bán kính đáy r=2 cm ⇒ Đường kính đáy là d = 4 cm
⇒ l=d=4cm
⇒ Thiết diện qua trục là tam giác đều cạnh 4 cm.
Bài 10: Thiết diện qua trục của một hình nón là tam giác vuông cân có cạnh huyền bằng 2√3. Thể tích của khối nón này là:
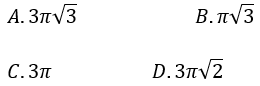
Lời giải:
Đáp án : B
Giải thích :
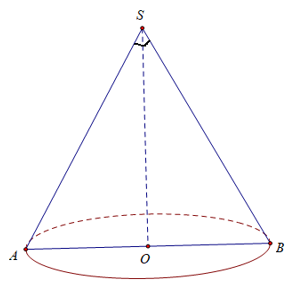
∆SAB vuông cân tại S có AB=2√3