Lý thuyết Hàm số lũy thừa - Toán lớp 12

Lý thuyết Hàm số lũy thừa

Tài liệu Lý thuyết Hàm số lũy thừa Toán lớp 12 sẽ tóm tắt kiến thức trọng tâm về Hàm số lũy thừa từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 12.

A. Tóm tắt lý thuyết

1. Định nghĩa: Hàm số y = x^α với α ∈ R được gọi là hàm số lũy thừa.

2. Tập xác định: Tập xác định của hàm số y = x^α là:

    • D = R nếu α là số nguyên dương.

    • D = R \ {0} với α nguyên âm hoặc bằng 0

    • D = (0; +∝) với α không nguyên.

3. Đạo hàm: Hàm số y = x^α có đạo hàm với mọi x > 0 và (x^α)' = α.x^{α - 1}.

4. Tính chất của hàm số lũy thừa trên khoảng (0; +∝).

y = xα, α > 0	y = xα, α < 0
a. Tập khảo sát: (0; +∝)	a. Tập khảo sát: (0; +∝)
b. Sự biến thiên + y' = αxα - 1 > 0, ∀x > 0 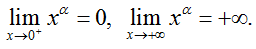+ Giới hạn đặc biệt + Tiệm cận: không có	b. Sự biến thiên + y' = αxα - 1 < 0, ∀x > 0 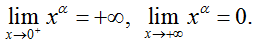+ Giới hạn đặc biệt + Tiệm cận: không có - Trục 0x là tiệm cận ngang - Trục 0y là tiệm cận đứng.
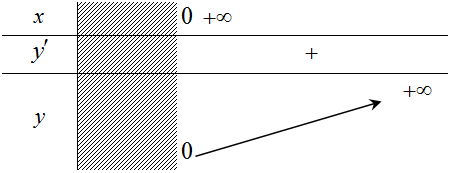
c. Bảng biến thiên	c. Bảng biến thiên

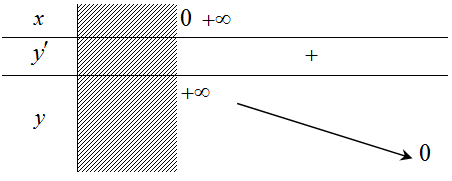
    d. Đồ thị:

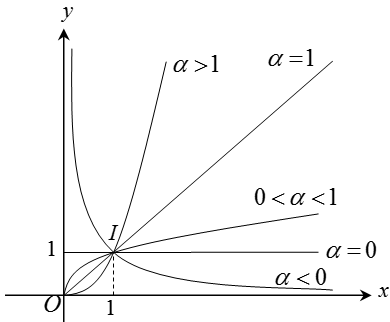
    Đồ thị của hàm số lũy thừa y = x^α luôn đi qua điểm I(1; 1)

    Lưu ý: Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó. Chẳng hạn: y = x³, y = x^-2, y = x^π

B. Kĩ năng giải bài tập

    Vận dụng thành thạo định nghĩa, tập xác định, cách tính đạo hàm, tính chất của hàm số lũy thừa.