Lý thuyết Hàm số mũ. Hàm số lôgarit - Toán lớp 12

Lý thuyết Hàm số mũ. Hàm số lôgarit

Tài liệu Lý thuyết Hàm số mũ. Hàm số lôgarit Toán lớp 12 sẽ tóm tắt kiến thức trọng tâm về Hàm số mũ. Hàm số lôgarit từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 12.

A. Tóm tắt lý thuyết

1. Hàm số mũ: y = a^x, (a > 0, a ≠ 1)

    1.1 Tập xác định: D = R

    1.2. Tập giá trị: T = (); +∝), nghĩa là khi giải phương trình mũ mà đặt t = a^f(x) thì t > 0

    1.3. Tính đơn điệu:

        + Khi a > 1 thì hàm số y = a^x đồng biến, khi đó ta luôn có: a^f(x) > a^g(x) ⇔ f(x) > g(x).

        + Khi 0 < a < 1 thì hàm số y = a^x nghịch biến, khi đó ta luôn có: a^f(x) > a^g(x) ⇔ f(x) < g(x).

    1.4. Đạo hàm:

    (a^x)' = a^x.ln a ⇒ (a^u)' = u'.a^u.ln a

    (e^x)' = e^x ⇒ (e^u)' = e^u.u'

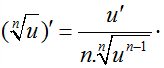
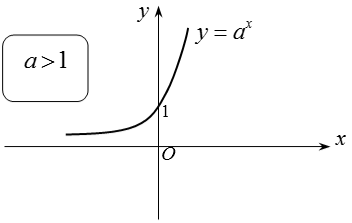
    1.5. Đồ thị: Nhận trục hoành làm đường tiệm cận ngang.

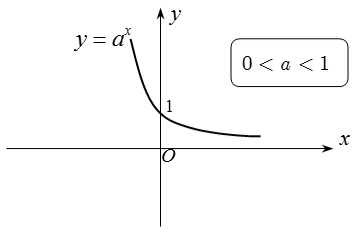
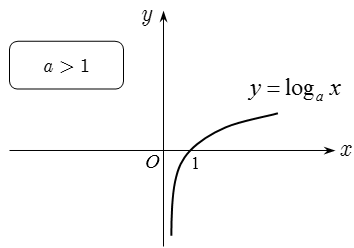
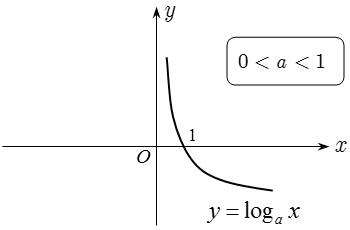
2. Hàm số logarit: y = log_ax, (a > 0, a ≠ 1)

    2.1 Tập xác định: D = (0; +∝)

    2.2. Tập giá trị: T = R, nghĩa là khi giải phương trình logarit mà đặt t = log_ax thì t không có điều kiện.

    2.3. Tính đơn điệu:

        + Khi a > 1 thì y = log_ax đồng biến trên D khi đó nếu: log_af(x) > log_ag(x) ⇔ f(x) > g(x).

        + Khi 0 < a < 1 thì y = log_ax nghịch biến trên D khi đó nếu log_af(x) > log_ag(x) ⇔ f(x) < g(x).

    2.4 Đạo hàm:

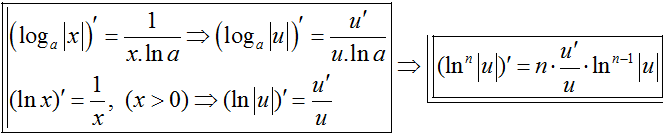
    2.5. Đồ thị: Nhận trục tung làm đường tiệm cận đứng.

B. Kĩ năng giải bài tập

    Vận dụng thành thạo định nghĩa, tập xác định, cách tính đạo hàm, tính chất của hàm số mũ và hàm số lôgarit