Lý thuyết Phương trình mũ và phương trình lôgarit - Toán lớp 12

Lý thuyết Phương trình mũ và phương trình lôgarit

Tài liệu Lý thuyết Phương trình mũ và phương trình lôgarit Toán lớp 12 sẽ tóm tắt kiến thức trọng tâm về Phương trình mũ và phương trình lôgarit từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 12.

A. Tóm tắt lý thuyết

1. PHƯƠNG TRÌNH MŨ.

1.1. Phương trình mũ cơ bản a^x = b (a > 0, a ≠ 1).

    ● Phương trình có một nghiệm duy nhất khi b > 0 .

    ● Phương trình vô nghiệm khi b ≤ 0 .

1.2. Biến đổi, quy về cùng cơ số

    a^f(x) = a^g(x) ⇔ a = 1 hoặc .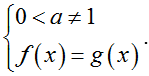

1.3. Đặt ẩn phụ

    f[a^g(x)] = 0 ( 0 < a ≠ 1) ⇔ .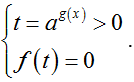

    Ta thường gặp các dạng:

    ● m.a^2f(x) + n.a^f(x) + p = 0

    ● m.a^f(x) + n.b^f(x) + p = 0, trong đó a.b = 1. Đặt t = a^f(x). t > 0, suy ra b^f(x) = 1/t.

    ● m.a^2f(x) + n.(a.b)^f(x) + p.b^2f(x) = 0. Chia hai vế cho b^2f(x) và đặt (a/b)^f(x) = t > 0.

1.4. Logarit hóa

    ● Phương trình .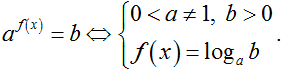

    ● Phương trình a^f(x) = b^g(x) ⇔ log_aa^f(x) = log_ab^g(x) ⇔ f(x) = g(x).log_ab

    hoặc log_ba^f(x) = log_bb^g(x) ⇔ f(x).log_ba = g(x)

1.5. Giải bằng phương pháp đồ thị

    o Giải phương trình: a^x = f(x) (0 < a ≠ 1) (*) .

    o Xem phương trình (*) là phương trình hoành độ giao điểm của hai đồ thị y = a^x (0 < a ≠ 1) và y = f(x) . Khi đó ta thực hiện hai bước:

    - Bước 1. Vẽ đồ thị các hàm số y = a^x (0 < a ≠ 1) và y = f(x) .

    - Bước 2. Kết luận nghiệm của phương trình đã cho là số giao điểm của hai đồ thị.

1.6. Sử dụng tính đơn điệu của hàm số

    o Tính chất 1. Nếu hàm số y = f(x) luôn đồng biến (hoặc luôn nghịch biến) trên (a; b) thì số nghiệm của phương trình f(x) = k trên (a; b) không nhiều hơn một và f(u) = f(v) ⇔ u = v, ∀u, v ∈ (a; b).

    o Tính chất 2. Nếu hàm số y = f(x) liên tục và luôn đồng biến (hoặc luôn nghịch biến) ; hàm số y = g(x) liên tục và luôn nghịch biến (hoặc luôn đồng biến) trên D thì số nghiệm trên D của phương trình f(x) = g(x) không nhiều hơn một.

    o Tính chất 3. Nếu hàm số y = f(x) luôn đồng biến (hoặc luôn nghịch biến) trên D thì bất phương trình f(u) > f(v) ⇔ u > v (hoặc u < v), ∀u,v ∈ D.

1.7. Sử dụng đánh giá

    o Giải phương trình f(x) = g(x).

    o Nếu ta đánh giá được .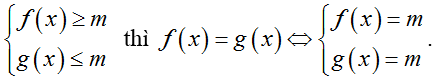

2. PHƯƠNG TRÌNH LÔGARIT

2.1. Biến đổi, quy về cùng cơ số

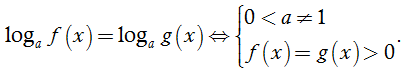
2.2. Đặt ẩn phụ

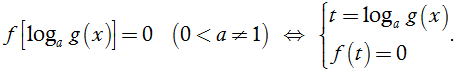
2.3. Mũ hóa hai vế

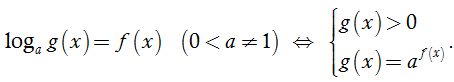
2.4. Phương pháp đồ thị

2.5. Sử dụng tính đơn điệu của hàm số