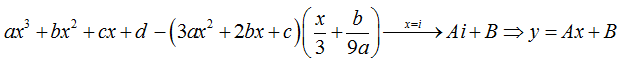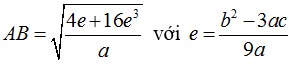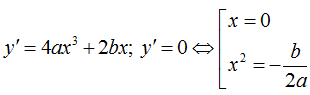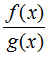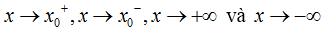Lý thuyết tổng hợp chương Ứng dụng đạo hàm để khảo sát hàm số - Toán lớp 12

Lý thuyết tổng hợp chương Ứng dụng đạo hàm để khảo sát hàm số

Tài liệu Lý thuyết tổng hợp chương Ứng dụng đạo hàm để khảo sát hàm số Toán lớp 12 sẽ tóm tắt kiến thức trọng tâm về Ứng dụng đạo hàm để khảo sát hàm số từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 12.

A. Tóm tắt các kỹ năng cơ bản

** SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ

1. Lập bảng xét dấu của một biểu thức P(x)

    Bước 1. Tìm nghiệm của biểu thức P(x), hoặc giá trị của x làm biểu thức P(x) không xác định.

    Bước 2. Sắp xếp các giá trị của x tìm được theo thứ tự từ nhỏ đến lớn.

    Bước 3. Sử dụng máy tính tìm dấu của P(x) trên từng khoảng của bảng xét dấu.

2. Xét tính đơn điệu của hàm số y = f(x) trên tập xác định

    Bước 1. Tìm tập xác định D.

    Bước 2. Tính đạo hàm y' = f'(x).

    Bước 3. Tìm nghiệm của f'(x) hoặc những giá trị x làm cho f'(x) không xác định.

    Bước 4. Lập bảng biến thiên.

    Bước 5. Kết luận.

3. Tìm điều kiện của tham số m để hàm số y = f(x) đồng biến, nghịch biến trên khoảng (a; b) cho trước.

    Cho hàm số y = f(x, m) có tập xác định D, khoảng (a; b) ⊂ D:

    - Hàm số nghịch biến trên (a; b) ⇔ y' ≤ 0, ∀ x ∈ (a; b)

    - Hàm số đồng biến trên (a; b) ⇔ y' ≥ 0, ∀ x ∈ (a; b)

* Chú ý.

    Riêng hàm số 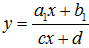thì :

    - Hàm số nghịch biến trên (a; b) ⇔ y' < 0, ∀ x ∈ (a; b)

    - Hàm số đồng biến trên (a; b) ⇔ y' > 0, ∀ x ∈ (a; b)

** CỰC TRỊ HÀM SỐ

1. Quy tắc tìm cực trị của hàm số

    - Quy tắc 1:

    Bước 1. Tìm tập xác định của hàm số.

    Bước 2. Tính f'(x) . Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.

    Bước 3. Lập bảng biến thiên.

    Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.

    - Quy tắc 2:

    Bước 1. Tìm tập xác định của hàm số.

    Bước 2. Tính f'(x). Giải phương trình f'(x) và ký hiệu x_i (i = 1; 2; 3;...) là các nghiệm của nó.

    Bước 3. Tính f"(x) và f"(x_i).

    Bước 4. Dựa vào dấu của f"(x_i) suy ra tính chất cực trị của điểm x_i.

2. Kỹ năng giải nhanh các bài toán cực trị hàm số bậc ba y = ax³ + bx² + cx + d (a ≠ 0)

    Ta có y'= 3ax² + 2bx + c

    - Đồ thị hàm số có hai điểm cực trị khi phương trình y' = 0 có hai nghiệm phân biệt ⇔ b² - 3ac > 0. Khi đó đường thẳng qua hai điểm cực trị đó là : .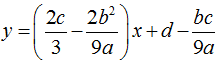

    - Bấm máy tính tìm ra đường thẳng đi qua hai điểm cực trị :

    Hoặc sử dụng công thức .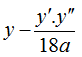

    - Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bậc ba là:

3. Kỹ năng giải nhanh các bài toán cực trị hàm trùng phương.

    Cho hàm số: y = ax⁴ + bx² + c (a ≠ 0) có đồ thị là (C).

    (C) có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt .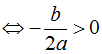

    Khi đó ba điểm cực trị là: 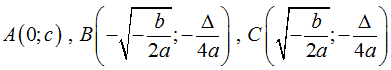với Δ = b² - 4ac

    Độ dài các đoạn thẳng: .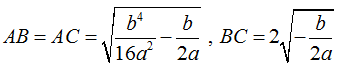

** GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ

1. Quy trình tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sử dụng bảng biến thiên

    - Bước 1. Tính đạo hàm f'(x).

    - Bước 2. Tìm các nghiệm của f'(x) và các điểm f'(x) trên K.

    - Bước 3. Lập bảng biến thiên của f(x) trên K.

    - Bước 4. Căn cứ vào bảng biến thiên kết luận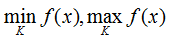

2. Quy trình tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số không sử dụng bảng biến thiên

    ** Trường hợp 1. Tập K là đoạn [a; b]

    - Bước 1. Tính đạo hàm f'(x) .

    - Bước 2. Tìm tất cả các nghiệm x_i ∈ [a; b] của phương trình f'(x) = 0 và tất cả các điểm α ∈ [a; b] làm cho f'(x) không xác định.

    - Bước 3. Tính f(a), f(b), f(x_i), f(α_i).

    - Bước 4. So sánh các giá trị tính được và kết luận .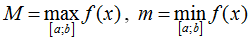

    ** Trường hợp 2. Tập K là khoảng (a; b)

    - Bước 1. Tính đạo hàm f'(x) .

    - Bước 2. Tìm tất cả các nghiệm x_i ∈ (a; b) của phương trình f'(x) = 0 và tất cả các điểm α_i ∈ (a; b) làm cho f'(x) không xác định.

    - Bước 3. Tính .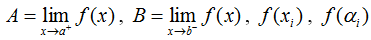

    - Bước 4. So sánh các giá trị tính được và kết luận .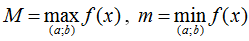

    ** Chú ý: Nếu giá trị lớn nhất (nhỏ nhất) là A hoặc B thì ta kết luận không có giá trị lớn nhất (nhỏ nhất).

** ĐƯỜNG TIỆM CẬN

1. Quy tắc tìm giới hạn vô cực

    Quy tắc tìm giới hạn của tích f(x).g(x)

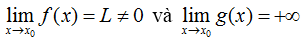
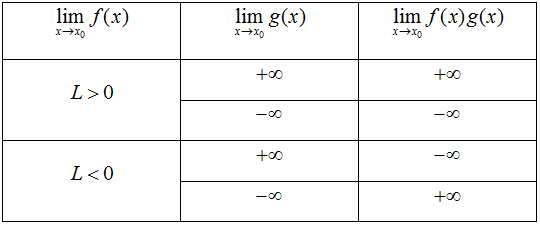
    Nếu (hoặc -∝) thì được tính theo quy tắc cho trong bảng sau:

    Quy tắc tìm giới hạn của thương

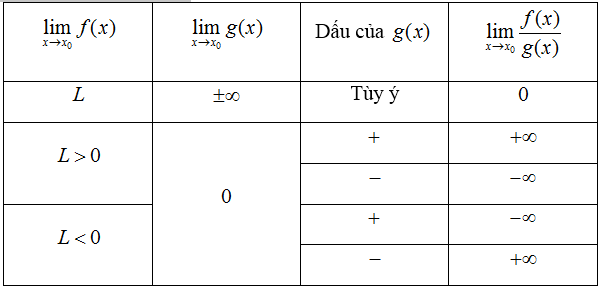
    (Dấu của g(x) xét trên một khoảng K nào đó đang tính giới hạn, với x ≠ x₀ )

2. Chú ý: Các quy tắc trên vẫn đúng cho các trường hợp

** KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THI HÀM SỐ

1. Sơ đồ bài toán khảo sát và vẽ đồ thị hàm số

    • Bước 1. Tìm tập xác định của hàm số;

    • Bước 2. Tính đạo hàm y' = f'(x) ;

    • Bước 3. Tìm nghiệm của phương trình ;

    • Bước 4. Tính giới hạn 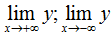và tìm tiệm cận đứng, ngang (nếu có);

    • Bước 5. Lập bảng biến thiên;

    • Bước 6. Kết luận tính biến thiên và cực trị (nếu có);

    • Bước 7. Tìm các điểm đặc biệt của đồ thị (giao với trục Ox, Oy, các điểm đối xứng, ...);

    • Bước 8. Vẽ đồ thị.

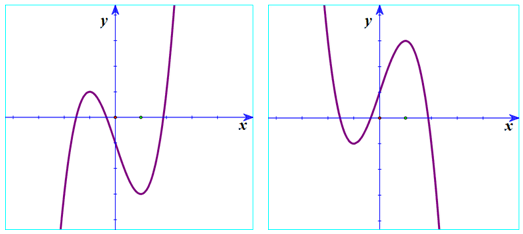
2. Các dạng đồ thị của hàm số bậc 3 y= ax³ + bx² + cx + d (a ≠ 0)

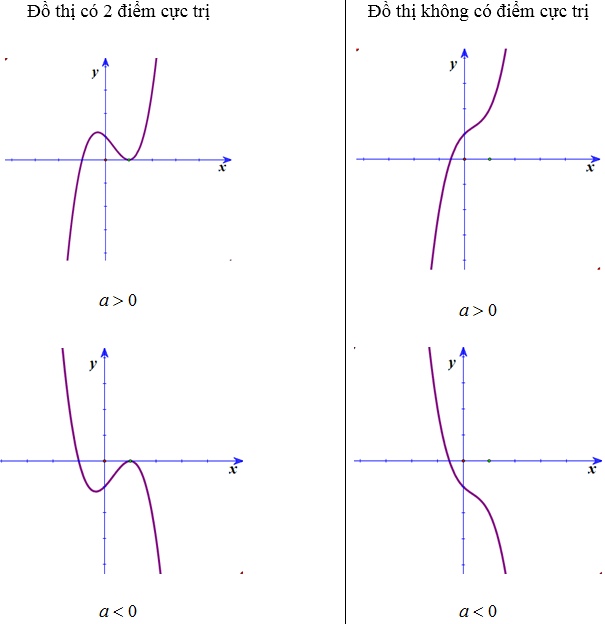
    - Lưu ý: Đồ thị hàm số có 2 điểm cực trị nằm 2 phía so với trục Oy khi ac < 0

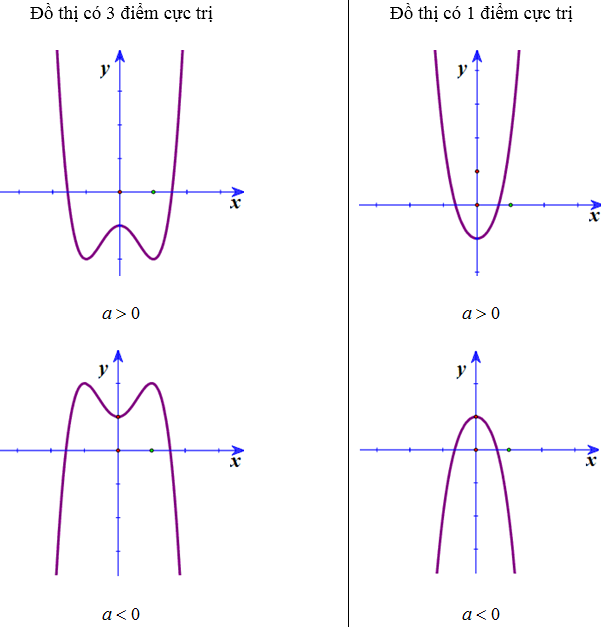
3. Các dạng đồ thị của hàm số bậc 4 trùng phương y = ax⁴ + bx² + c (a ≠ 0)

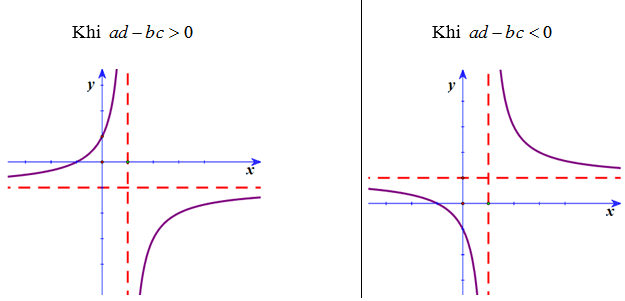
4. Các dạng đồ thị của hàm số nhất biến 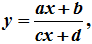(ab - bc ≠ 0)

5. Biến đổi đồ thị

    Cho hàm số y = f(x) có đồ thị (C) . Khi đó, với số a > 0 ta có:

    • Hàm số y = f(x) + a có đồ thị (C') là tịnh tiến (C) theo phương của Oy lên trên a đơn vị.

    • Hàm số y = f(x) - a có đồ thị (C') là tịnh tiến (C) theo phương của Oy xuống dưới a đơn vị.

    • Hàm số y = f(x + a) có đồ thị (C') là tịnh tiến (C) theo phương của Ox qua trái a đơn vị.

    • Hàm số y = f(x - a) có đồ thị (C') là tịnh tiến (C) theo phương của Ox qua phải a đơn vị.

    • Hàm số y = -f(x) có đồ thị (C') là đối xứng của (C) qua trục Ox.

    • Hàm số y = f(-x) có đồ thị (C') là đối xứng của (C) qua trục Oy.

    • Hàm số 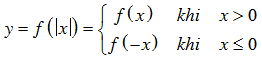có đồ thị (C') bằng cách:

    - Giữ nguyên phần đồ thị (C) nằm bên phải trục Oy và bỏ phần (C) nằm bên trái Oy.

    - Lấy đối xứng phần đồ thị (C) nằm bên phải trục Oy qua Oy.

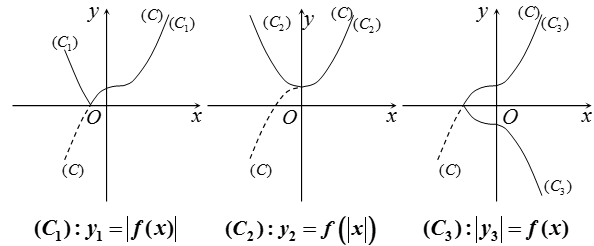
    • Hàm số 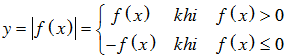có đồ thị (C') bằng cách:

    - Giữ nguyên phần đồ thị (C) nằm trên Ox.

    - Lấy đối xứng phần đồ thị (C) nằm dưới Ox qua Ox và bỏ phần đồ thị (C) nằm dưới Ox.