Nếu đặt u = ln(x+2) và dv = xdx thì tích phân

Câu hỏi:

Nếu đặt $\{\begin{cases} u = \ln (x + 2) \\ d v = x d x \end{cases}$ thì tích phân $I = \int_{0}^{1} x . \ln (x + 2) d x$ trở thành:

A. $I = \frac{x^{2} \ln (x + 2)}{2} |_{0}^{1} - \frac{1}{2} \int_{0}^{1} \frac{x^{2}}{x + 2} d x$

B. $I = x^{2} \ln (x + 2) |_{0}^{1} - \frac{1}{4} \int_{0}^{1} \frac{x^{2}}{x + 2} d x$

C. $I = \frac{x^{2} \ln (x + 2)}{2} |_{0}^{1} + \int_{0}^{1} \frac{x^{2}}{x + 2} d x$

D. $I = \frac{x^{2} \ln (x + 2)}{4} |_{0}^{1} - \frac{1}{4} \int_{0}^{1} \frac{x^{2}}{x + 2} d x$

Trả lời:

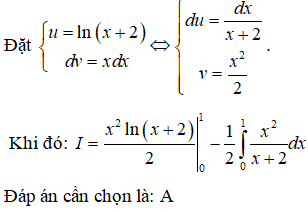
Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Tích phân $\int_{0}^{3} x (x - 1) d x$ có giá trị bằng với giá trị của tích phân nào trong các tích phân dưới đây?

Xem lời giải »

Câu 2:

Tích phân $I = \int_{1}^{e} 2 x (1 - \ln x) d x$ bằng:

Xem lời giải »

Câu 3:

Biết rằng $\int_{1}^{a} \ln x d x = 1 + 2 a (a > 1)$ . Khẳng định nào dưới đây là khẳng định đúng?

Xem lời giải »

Câu 4:

Tính tích phân $I = \int_{1}^{2} \ln (x + 1) d x$

Xem lời giải »

Câu 5:

Cho hàm số f (x) có f (2) = 0 và $f' (x) = \frac{x + 7}{\sqrt{2 x - 3}} \forall x \in (\frac{3}{2}; + \infty)$ . Biết rằng $\int_{4}^{7} f (\frac{x}{2}) d x = \frac{a}{b}$ (a,b thuộc Z, b>0, $\frac{a}{b}$ là phân số tối giản). Khi đó a +b bằng:

Xem lời giải »

Câu 6:

Cho tích phân $I = \int_{0}^{\frac{π}{4}} \frac{x^{2}}{(x s i n x + c o s x)} d x = \frac{m - π}{m + π}$ , giá trị của m bằng:

Xem lời giải »

Câu 7:

Biết $\int_{0}^{\frac{π}{3}} \frac{x^{2} d x}{(x s i n x + c o s x)^{2}} = - \frac{a π}{b + c π \sqrt{3}} + d \sqrt{3}$ với $a, b, c, d \in Z^{+}$ . Tính P=a+b+c+d

Xem lời giải »

Câu 8:

Cho hàm số f (x) liên tục trên R thỏa mãn điều kiện $x . f (x^{3}) + f (x^{2} - 1) = {e^{x}}^{2}, \forall x \in R$ . Khi đó giá trị của $\int_{- 1}^{0} f (x) d x$ là:

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Nếu đặt u = ln(x+2) và dv = xdx thì tích phân

Xem thêm bài tập Toán có lời giải hay khác: