Phần thực và phần ảo của số phức z thỏa mãn: (1 + i)^2(2 - i) z = 8 + i + (1 + 2i)z lần lượt là?

Câu hỏi:

Phần thực và phần ảo của số phức z thỏa mãn: (1 + i)²(2 - i) z = 8 + i + (1 + 2i)z lần lượt là?

A. -3; -2

B. 2; 3

C. 2; -3

D. Đáp án khác.

Trả lời:

Chọn C.

Ta có: ( 1 + i)²(2 - i) z = 8 + i + (1 + 2i)z

Nên z[( 1 + i)²(2 -i) – (1 + 2i) ] = 8 + i

Suy ra: z[2i(2 - i) – 1 - 2i] = 8 + i

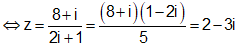
Vậy số phức z đã cho có phần thực là 2, phần ảo là -3.

Câu 1:

Phần ảo của số z thỏa mãn phương trình: ( z + 2)i = ( 3i - z)( -1 + 3i) gần với giá trị nào nhất.

Câu 2:

Cho phương trình sau: $(2 i z - 3) (z - 5 i) (\bar{z} - 3 + 6 i) = 0$ .Tính tổng tất cả các phần thực của các nghiệm của phương trình.

Câu 3:

Cho số phức z thỏa mãn ( 3+ i) z = 2. Tính mô-đun của số phức w = z + $\frac{2}{5}$ - $\frac{4}{5}$ i.

Câu 4:

Cho số phức z thỏa mãn điều kiện $(2 + i) z + \frac{1 - i}{1 + i} = 5 - i$ . Tìm phần thực của số phức w = 4z

Câu 5:

Số phức z thỏa mãn phương trình $(2 - 3 i) z + (4 + i) \bar{z} = - {(1 + 3 i)}^{2}$ có phần thực và phần ảo lần lượt là:

Câu 6:

Tìm phần thực của số phức $\frac{25 i}{z}$ , biết rằng $\frac{z}{2 - i} + (4 - 3 i) \bar{z} = 26 + 6 i$

Câu 7:

Có bao nhiêu số phức z thỏa |z| = 2 và z³ là số thực là:

Câu 8:

Xác định tập hợp các điểm trong mặt phẳng biểu diễn số phức z thoả điều kiện |z + 1 – 3i| ≤ 4.

Các dạng bài tập Toán lớp 12