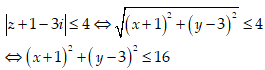Xác định tập hợp các điểm trong mặt phẳng biểu diễn số phức z thoả điều kiện |z + 1 – 3i| ≤ 4

Câu hỏi:

Xác định tập hợp các điểm trong mặt phẳng biểu diễn số phức z thoả điều kiện |z + 1 – 3i| ≤ 4.

A. Hình tròn tâm I(-1;3), bán kính r = 4.

B. Đường tròn tâm I(-1;3), bán kính r = 4.

C. Hình tròn tâm I(-1; -3), bán kính r = 4.

D. Đường tròn tâm I(1;3), bán kính r = 4.

Trả lời:

Chọn A.

Giả sử z = x + yi, ta có z + 1 - 3i = x + 1 + (y - 3)i.

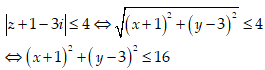
Vậy tập hợp các điểm trong mặt phẳng biểu diễn số phức z là hình tròn tâm I(-1; 3), bán kính r = 4.

Câu 1:

Phần ảo của số z thỏa mãn phương trình: ( z + 2)i = ( 3i - z)( -1 + 3i) gần với giá trị nào nhất.

Câu 2:

Cho phương trình sau: $(2 i z - 3) (z - 5 i) (\bar{z} - 3 + 6 i) = 0$ .Tính tổng tất cả các phần thực của các nghiệm của phương trình.

Câu 3:

Cho số phức z thỏa mãn ( 3+ i) z = 2. Tính mô-đun của số phức w = z + $\frac{2}{5}$ - $\frac{4}{5}$ i.

Câu 4:

Cho số phức z thỏa mãn điều kiện $(2 + i) z + \frac{1 - i}{1 + i} = 5 - i$ . Tìm phần thực của số phức w = 4z

Câu 5:

Giá trị của i¹⁰⁵+ i²³+ i²⁰- i³⁴ là ?

Câu 6:

Với mọi số ảo z, số z² + |z|² là :

Câu 7:

Cho số phức z thỏa mãn: $3 z + 2 \bar{z} = {(4 - i)}^{2}$ . Môđun của số phức z là

Câu 8:

Tìm số phức z , biết $z - (2 + 3 i) \bar{z} = 1 - 9 i$

Các dạng bài tập Toán lớp 12