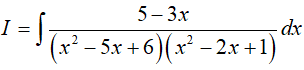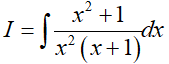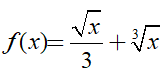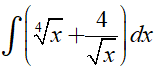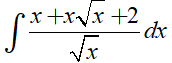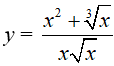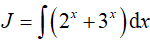Phương pháp tính nguyên hàm của các hàm số cơ bản cực hay - Toán lớp 12

---

Phương pháp tính nguyên hàm của các hàm số cơ bản cực hay

Với Phương pháp tính nguyên hàm của các hàm số cơ bản cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính nguyên hàm của các hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng 1.1. Hàm đa thức

1. Phương pháp giải

Để tính nguyên hàm của các hàm đa thức ta cần sử dụng các công thức sau:

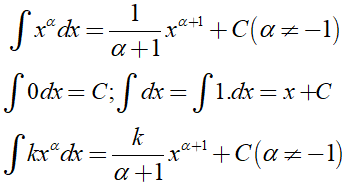
Trong đó, k là hằng số.

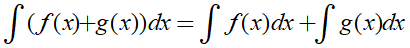
2. Ví dụ minh họa

Ví dụ 1. Họ nguyên hàm của hàm số f(x)= x² − 2x + x⁻² là

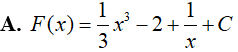
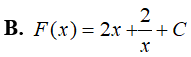
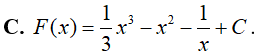
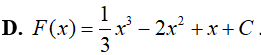
Lời giải:

Đáp án: C

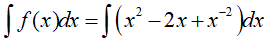
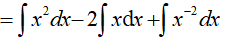
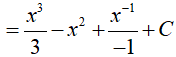
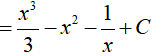
Ví dụ 2. Trong các hàm số sau đây, hàm số nào là một nguyên hàm của hàm số: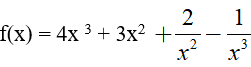

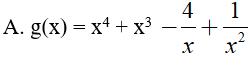
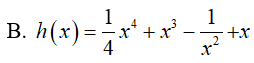
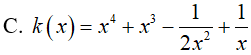
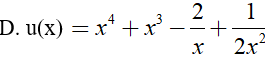
Lời giải:

Đáp án: D

Ta có:

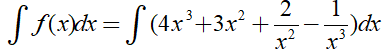
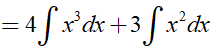
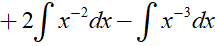
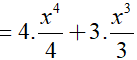
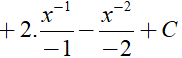
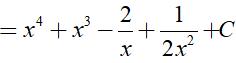
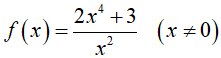
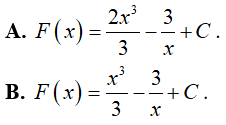
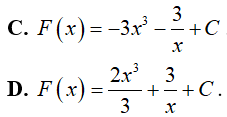
Ví dụ 3. Nguyên hàm F(x) của hàm số là

Lời giải:

Đáp án: A

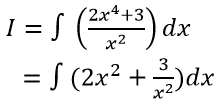
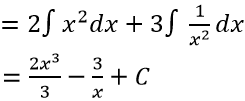
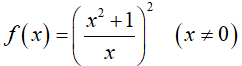
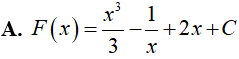
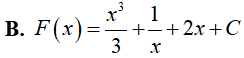
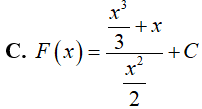
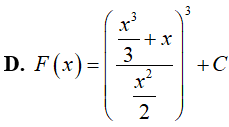
Ví dụ 4. Nguyên hàm F(x) của hàm số là

Lời giải:

Đáp án: A

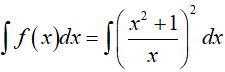
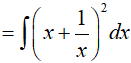
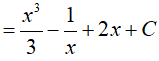
Ví dụ 5. Tìm hàm số f(x) biết rằng f'(x) = 2x + 1 và f(1) = 5?

A. x² + x + 3     B. x² + x − 3     C. x² + x     D. x² − x.

Lời giải:

Đáp án: A

Theo giả thiết ta có:

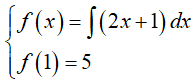
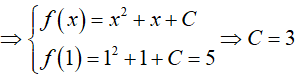
Vậy hàm số cần tìm là f(x) = x² + x + 3

Dạng 1.2. Hàm phân thức

1. Phương pháp giải

Để tìm nguyên hàm của các hàm phân thức ta cần sử dụng các công thức sau:

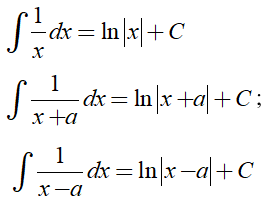
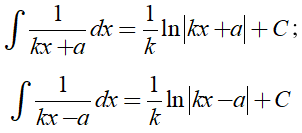
2. Ví dụ minh họa

Ví dụ 1. Cho 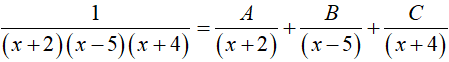Khi đó tổng S = A + B + C bằng

Lời giải:

Đáp án: B

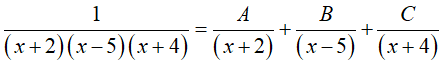
=> A(x − 5)(x + 4) + B(x + 2)(x + 4) + C(x + 2)(x − 5) = 1

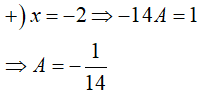
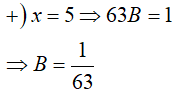
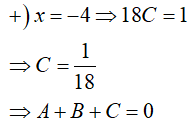
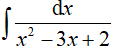
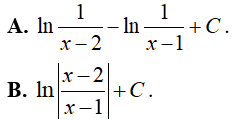
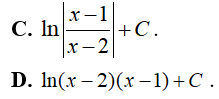
Ví dụ 2. Tìm là:

Lời giải:

Đáp án: B

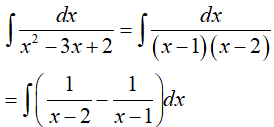
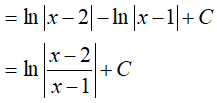
Ví dụ 3. Cho 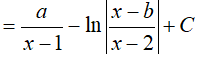Khi đó P = 2a + b bằng:

A. 0     B. 1     C. 2     D. 3

Lời giải:

Đáp án: B

Ta có:

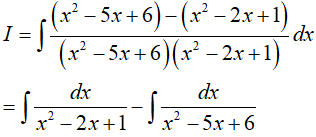
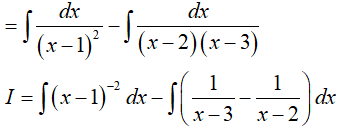
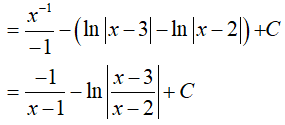
Suy ra a = −1; b = 3 => P = 2a + b = 1

Ví dụ 4. Cho 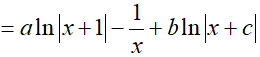. Khi đó P = 2(a + b)c bằng

A. 2     B. −2     C. 1     D. 0

Lời giải:

Đáp án: D

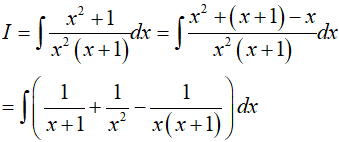
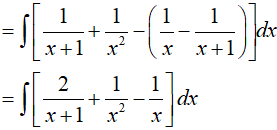
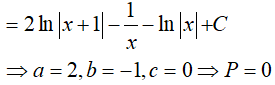
Suy ra a = −1; b = 3 => P = 2a + b = 1

Ví dụ 5. Tìm hàm số f(x)= x² + ax + ln |bx+ 1| + c biết 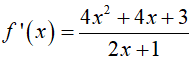và f(0) = 1. Khi đó S = (2a − b)³.c bằng

Lời giải:

Đáp án: A

Ta có:

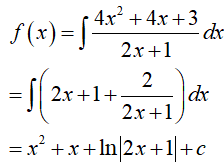
Mà f(0) = 1 nên c = 1. Khi đó, f(x)= x² + x+ ln|2x+ 1| +1

Suy ra, a = 1, b = 2 và c = 1 nên S = (2a − b)³c= 0

Dạng 1.3. Hàm chứa căn thức

1. Phương pháp giải

Để tìm nguyên hàm của các hàm chứa căn thức ta cần linh hoạt sử dụng các công thức sau:

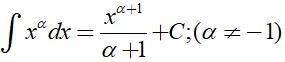
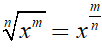
2. Ví dụ minh họa

Ví dụ 1. Tìm nguyên hàm của hàm số

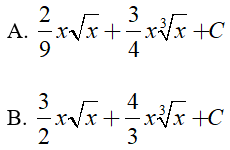
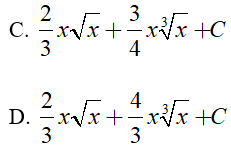
Lời giải:

Đáp án: A

Ta có:

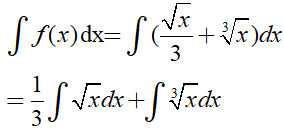
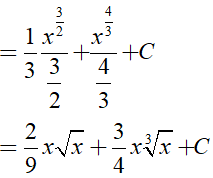
Ví dụ 2. Tìm

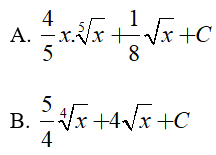
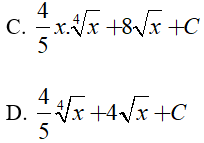
Lời giải:

Đáp án: C

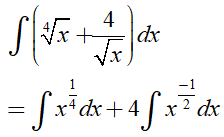
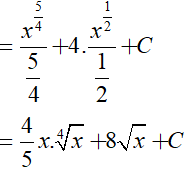
Ví dụ 3. Tìm

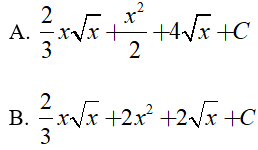
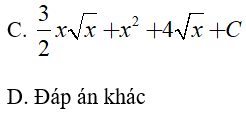
Lời giải:

Đáp án: A

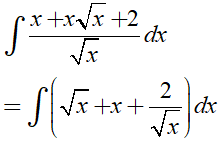
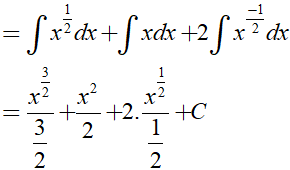
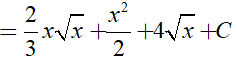
Ví dụ 4. Nguyên hàm của hàm số:

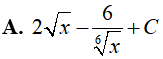
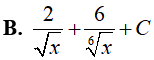
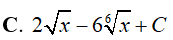
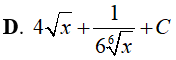
Lời giải:

Đáp án: A

Ta có:

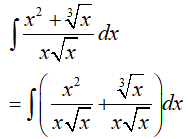
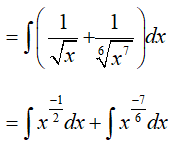
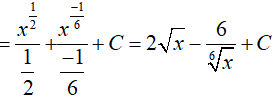
Dạng 1.4. Hàm lượng giác

1. Phương pháp giải

Để tìm nguyên hàm của hàm số lượng giác ta cần sử dụng các công thức sau:

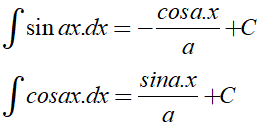
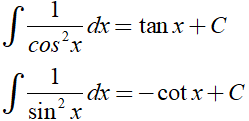
Ngoài ra, ta cần sử dụng các tính chất của nguyên hàm; các công thức cộng, công thức nhân đôi, công thức biến đổi tích thành tổng, công thức hạ bậc...

2. Ví dụ minh họa

Ví dụ 1. Nguyên hàm của hàm số f(x) = 4cos4x là

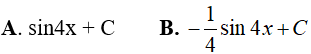
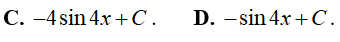
Lời giải:

Đáp án: A

Ta có:

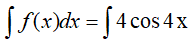
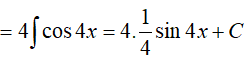
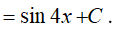
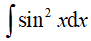
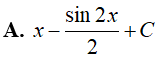
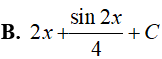
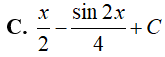
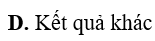
Ví dụ 2. Tính , kết quả là:

Lời giải:

Đáp án: C

Ta có:

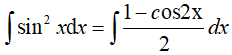
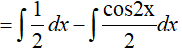
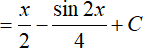
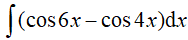
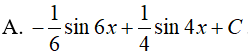
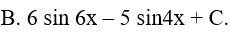
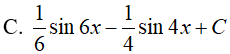
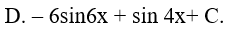
Ví dụ 3. Tính , kết quả là:

Lời giải:

Đáp án: C

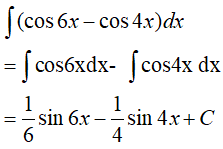
Ví dụ 4. Một nguyên hàm của hàm số f(x) = sinx . cosxlà:

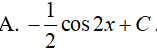
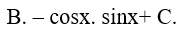
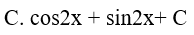
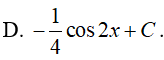
Lời giải:

Đáp án: D

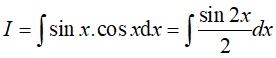
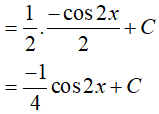
Ví dụ 5. Một nguyên hàm của hàm số f(x)= cos5x. cosx là:

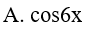
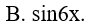
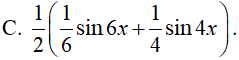
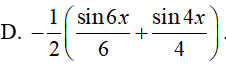
Lời giải:

Đáp án: C

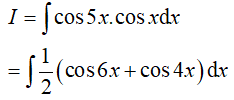
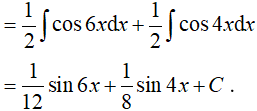
Dạng 1.5. Hàm số mũ, logarit

1. Phương pháp giải

Để tìm nguyên hàm của các hàm số mũ ta cần sử dụng các công thức sau:

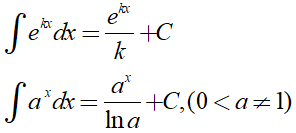
Ngoài ra, ta còn sử dụng tính chất của nguyên hàm, tính chất của lũy thừa, hàm số mũ.

2. Ví dụ minh họa

Ví dụ 1. Tìm

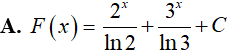
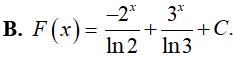
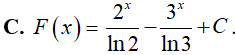
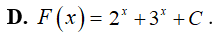
Lời giải:

Đáp án: A

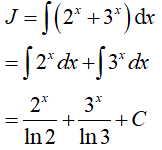
Ví dụ 2. Nguyên hàm của hàm số f(x) = e^x.( 2 − e^−x ) là

A. 2e^x + x + C.     B. e^x + e^−x + C.    

C. 2e^x − x+ C.     D. 2e^x + 2x + C.

Lời giải:

Đáp án: C

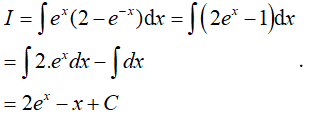
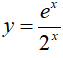
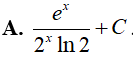
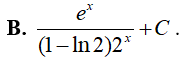
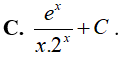
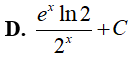
Ví dụ 3. Nguyên hàm của hàm số là

Lời giải:

Đáp án: B

Ta có:

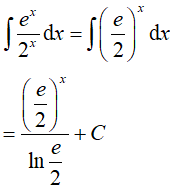
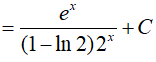
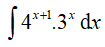
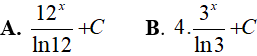
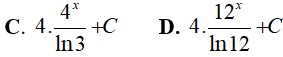
Ví dụ 4. Tính , kết quả là:

Lời giải:

Đáp án: D

Ta có:

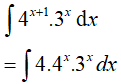
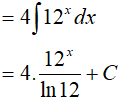
Ví dụ 5. Kết quả nào sai trong các kết quả sau:

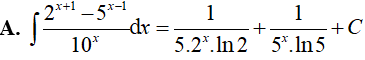
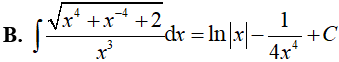
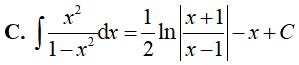
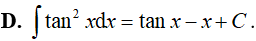
Lời giải:

Đáp án: A

Ta xét các phương án:

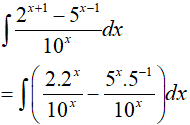
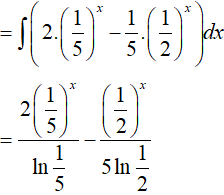
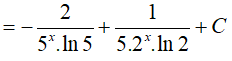
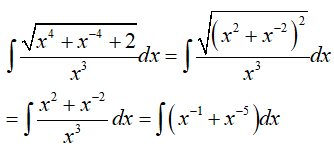
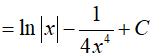
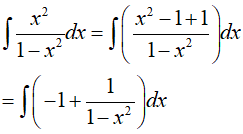
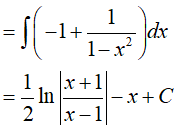
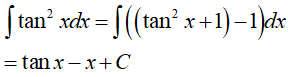
Vậy phương án A sai.