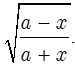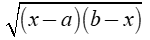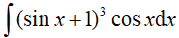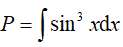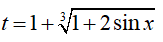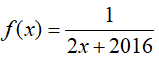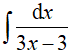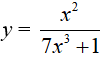Phương pháp tính nguyên hàm đổi biến số cực hay - Toán lớp 12
Phương pháp tính nguyên hàm đổi biến số cực hay
Với Phương pháp tính nguyên hàm đổi biến số cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính nguyên hàm đổi biến số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Để tìm nguyên hàm của hàm số ta có thể dùng phương pháp đổi biến số. Phương pháp này chúng ta có hai hướng đổi biến số:
+ Hướng 1:
• Bước 1: Chọn t = φ(x) . Trong đó φ(x) là hàm số mà ta chọn thích hợp .
• Bước 2: Tính vi phân hai vế: dt = φ'(t)dt .
• Bước 3: Biểu thị: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt .
• Bước 4: Khi đó:
*Hướng 2:
• Bước 1: Chọn x = φ(t), trong đó φ(t) là hàm số mà ta chọn thích hợp .
• Bước 2: Lấy vi phân hai vế: dx = φ'(t)dt
• Bước 3: Biến đổi: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt
• Bước 4: Khi đó tính: 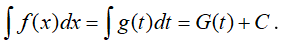
Dạng 2.1. Hàm đa thức
2. Ví dụ minh họa
Ví dụ 1. Nguyên hàm của hàm số f(x) = ( 3x + 2)3 là:
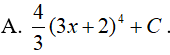
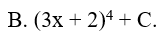
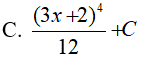
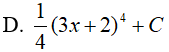
Lời giải:
Đáp án: C
Ta có:
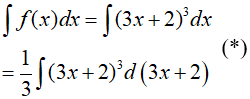
Đặt t = 3x + 2; khi đó ta có;
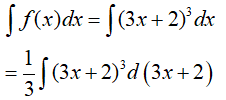
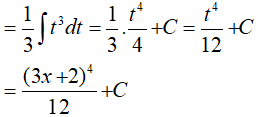
Ví dụ 2. Nguyên hàm của hàm số f(x)= (1 − 2x)5 là:
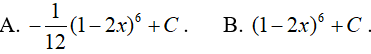
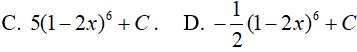
Lời giải:
Đáp án: A
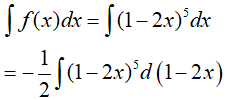
Đặt t = 1 − 2x, khi đó ta có:
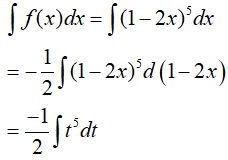
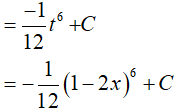
Ví dụ 3. Tính nguyên hàm 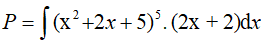
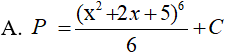
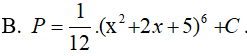
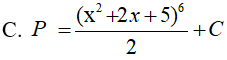
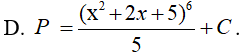
Lời giải:
Đáp án: B
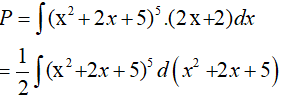
Đặt t = x2 + 2x + 5 , khi đó ta có:
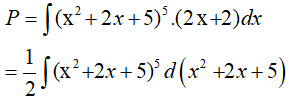
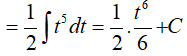
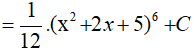
Ví dụ 4. Tính 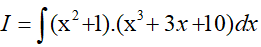
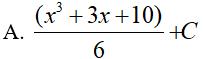
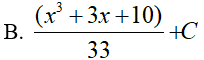
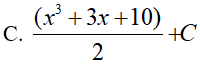
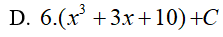
Lời giải:
Đáp án: A
Ta có:
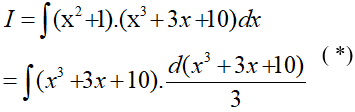
Đặt t = x3 + 3x + 10, khi đó (*) trở thành:
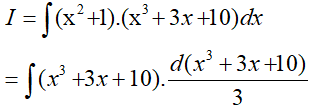
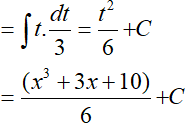
Ví dụ 5. Tính 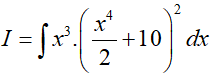
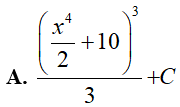
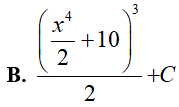
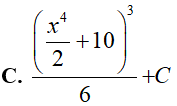
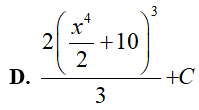
Lời giải:
Đáp án: C
Ta có:
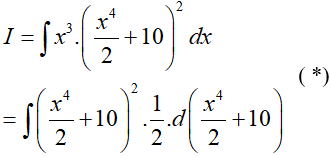
Đặt 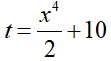
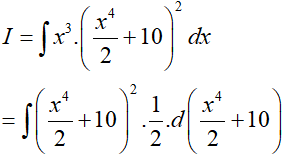
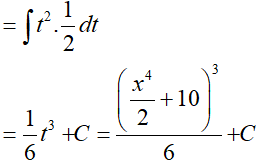
Dạng 2.2. Hàm phân thức
2. Ví dụ minh họa
Ví dụ 1. Tính 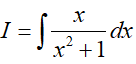
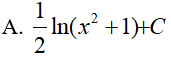
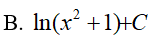
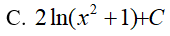
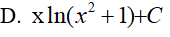
Lời giải:
Đáp án: A
Ta có:
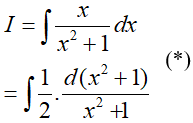
Đặt t = x2 + 1, khi đó (*) trở thành:
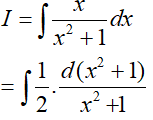
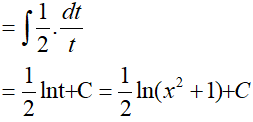
Ví dụ 2. Cho 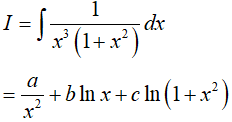


Lời giải:
Đáp án: B
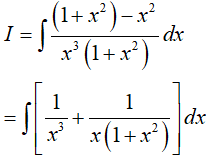
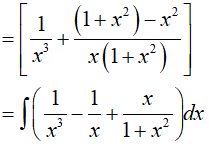
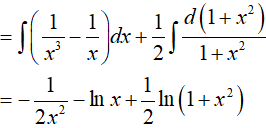
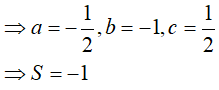
Ví dụ 3. Nguyên hàm của 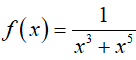
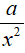
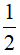

Lời giải:
Đáp án: D
Ta có:
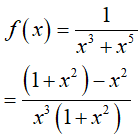
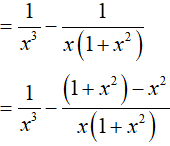
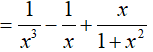
Vậy
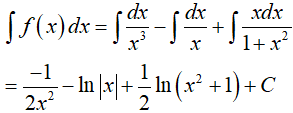
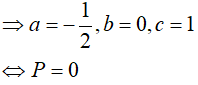
Ví dụ 4. Tìm hàm số f(x) = x2 + ax + ln|bx + 1| + c biết 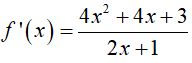


Lời giải:
Đáp án: A
Ta có:
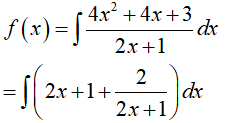
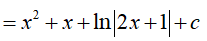
Vì
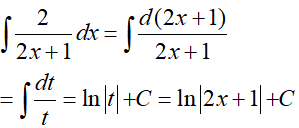
Mà
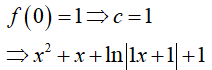
Suy ra, a= 1, b= 2, c= 1 nên S = (2a − b)3 . c = 0
Ví dụ 5. 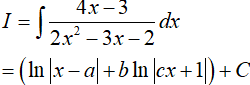
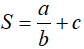
A. 2 B. −2 C. 4 D. 3
Lời giải:
Đáp án: C
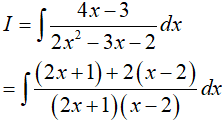
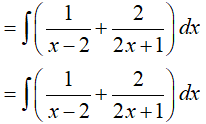
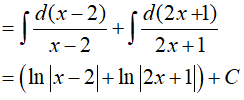
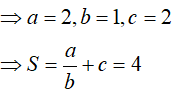
Dạng 2.3. Hàm chứa căn thức
1. Phương pháp giải
Dấu hiệu |
Cách chọn |
√(a2 − x2) |
Đặt x = |a|. sint; với |
√(x2 − a2) |
Đặt |
√(a2 + a2) |
Đặt x= |a|. tant; với |
|
Đặt x= acos2t |
Đặt x = a + (b − a)sin2t |
2. Ví dụ minh họa
Ví dụ 1. Kết quả của 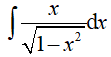
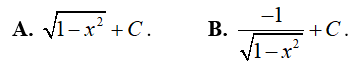
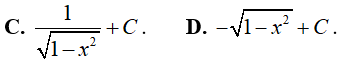
Lời giải:
Đáp án: D
Đặt
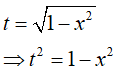
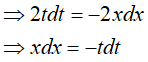
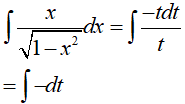
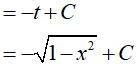
Ví dụ 2. Một nguyên hàm của hàm số y = x√(1 + x2) là:
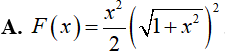
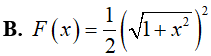
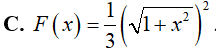
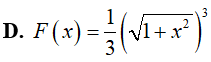
Lời giải:
Đáp án: D
Đặt
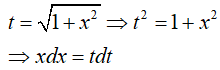
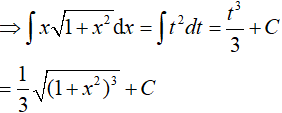
Vậy
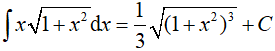
Ví dụ 3. Nguyên hàm của hàm số: 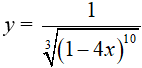
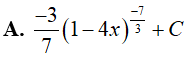
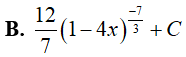
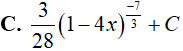
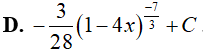
Lời giải:
Đáp án: C
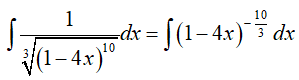
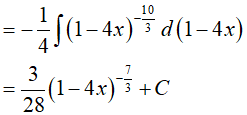
Đặt t = 1 − 4x, khi đó(*) trở thành :
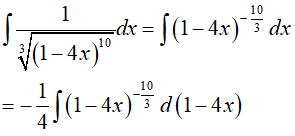
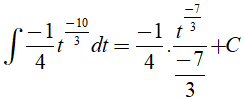
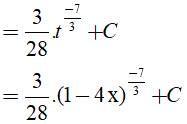
Ví dụ 4. Một nguyên hàm của hàm số: 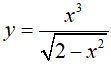
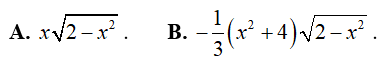
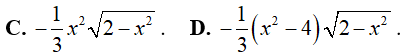
Lời giải:
Đáp án: B
Đặt √(2 − x2) = t => x2 = 2 − t2 => xdx = −tdt
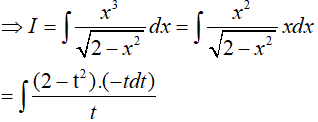
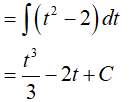
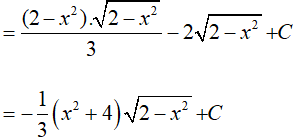
Ví dụ 5. Cho 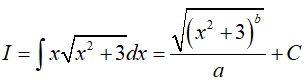
A. 2018 B. 2020 C. 2025 D. 2030
Lời giải:
Đáp án: A
Đặt √(x2 + 3) => t2 = x2 + 3 => 2tdt = 2xdx => xdx = tdt
Suy ra:
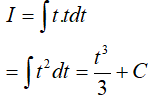
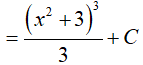
Do đó, b = 3, a = 3
Vậy S = logb2a + logab + 2016 = 2018
Dạng 2.4. Hàm lượng giác
2. Ví dụ minh họa
Ví dụ 1. Tìm
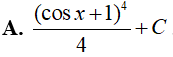
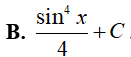
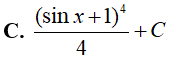
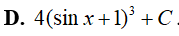
Lời giải:
Đáp án: C
Ta có :
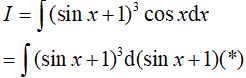
Đặt t = sinx + 1, từ (*) suy ra:
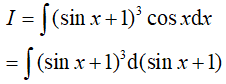
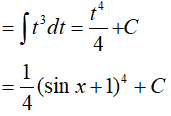
Ví dụ 2. Tìm
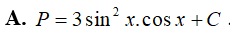
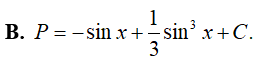
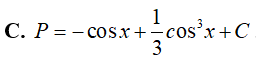
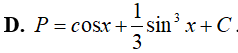
Lời giải:
Đáp án: C
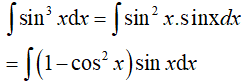
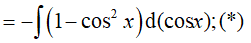
Đặt t= sin x, khi đó (*) trở thành:
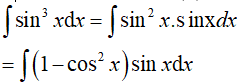
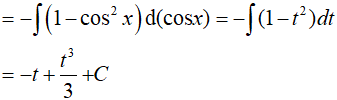
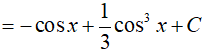
Ví dụ 3. Tìm
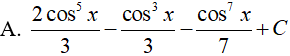
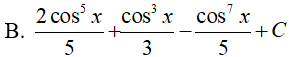
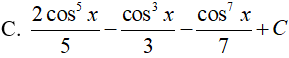
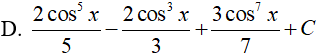
Lời giải:
Đáp án: C
Vì lũy thừa của sin là số lẻ nên ta đổi biến u = cosx => du = (cosx)'dx.
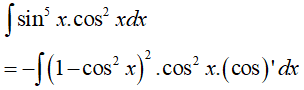
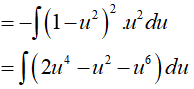
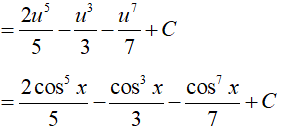
Ví dụ 4. Tìm nguyên hàm:
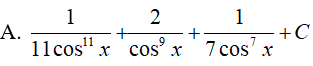
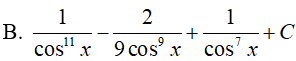
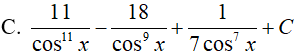
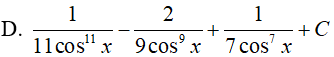
Lời giải:
Đáp án: D
Ta có:
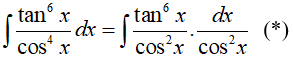
Đặt u= tanx => 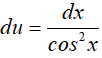
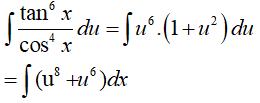
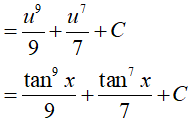
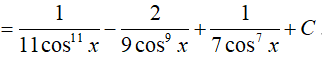
Ví dụ 5. Tìm
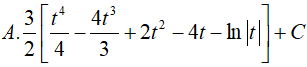
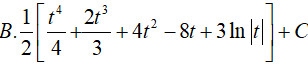
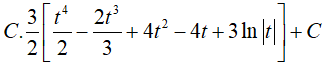
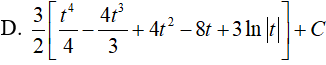
Lời giải:
Đáp án: D
Ta có:
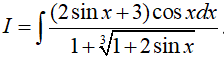
Đặt
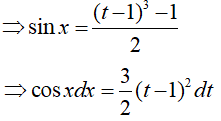
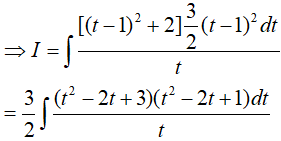
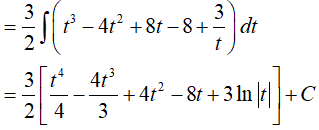
Dạng 2.5. Hàm mũ, logarit
2. Ví dụ minh họa
Ví dụ 1. Trong các hàm số sau đây, hàm số nào là một nguyên hàm của
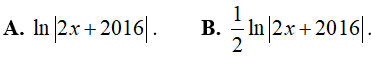
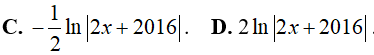
Lời giải:
Đáp án: B
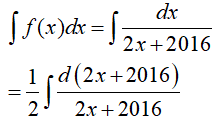
Đặt t= 2x+ 2016, khi đó (*) trở thành:
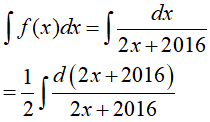
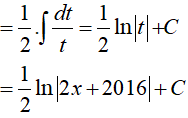
Ví dụ 2. Tìm
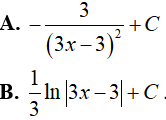
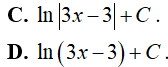
Lời giải:
Đáp án: B
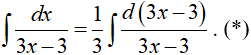
Đặt t= 3x − 3, khi đó (*) trở thành:
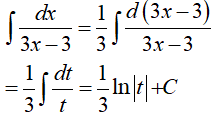
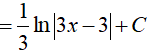
Ví dụ 3. Một nguyên hàm của hàm số
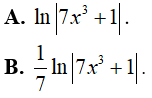
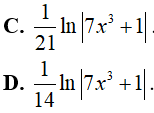
Lời giải:
Đáp án: C
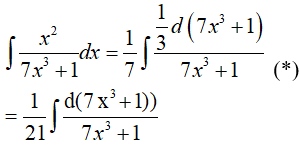
Đặt t= 7x3 + 1, khi đó (*) trở thành:
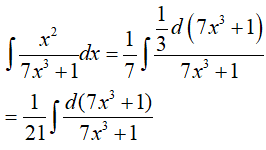
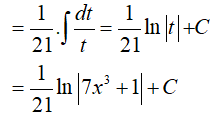
Ví dụ 4. Trong các mệnh đề sau đây mệnh đề nào đúng ?
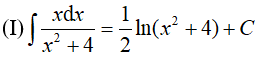
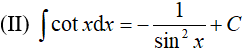
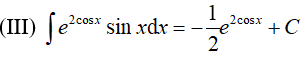
A. Chỉ (I). B. Chỉ (III). C. Chỉ (I) và (II). D. Chỉ (I) và (III).
Lời giải:
Đáp án: D
Ta tìm nguyên hàm của các hàm số:
(I):
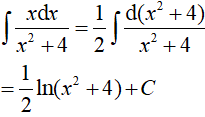
(II):
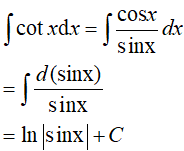
(III):
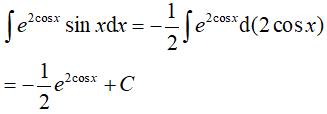
Do đó, (I) và (III) đúng.
Ví dụ 5. Một nguyên hàm của hàm số
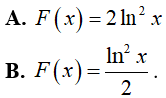
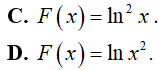
Lời giải:
Đáp án: D
Ta có:
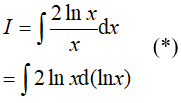
Đặt t = lnx, khi đó (*) trở thành:
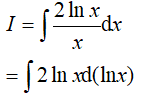
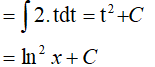

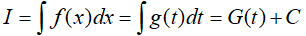
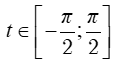 hoặc x= |a|. cost; với t ∈ [0; π]
hoặc x= |a|. cost; với t ∈ [0; π] 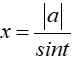 ; với
; với 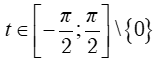 hoặc
hoặc 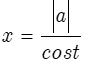 ; với
; với 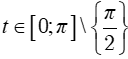
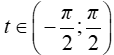 hoặc x = |a|.cot t; với t ∈ (0; π)
hoặc x = |a|.cot t; với t ∈ (0; π)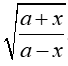 hoặc
hoặc