Phương pháp tính thể tích các khối đa diện cực hay - Toán lớp 12

Phương pháp tính thể tích các khối đa diện cực hay

Với Phương pháp tính thể tích các khối đa diện cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính thể tích các khối đa diện từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

+ Ta có thể: Phân chia khối đa diện đã cho thành các khối chóp khác, dùng tỉ số thể tích....

2. Ví dụ minh họa

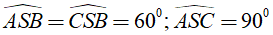
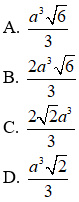
Ví dụ 1. Cho hình chóp tam giác S.ABC có ; SA= SB= SC =2a. Tính thể tích khối chóp S.ABC

Hướng dẫn giải

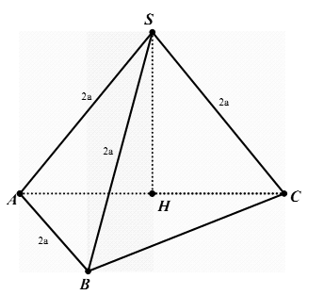
+ Tam giác SAB có SA= SB nên tam giác này là tam giác cân. Mà 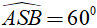nên tam giác SAB là tam giác đều => AB=2a.

+ Tương tự tam giác SBC là tam giác đều nên BC= 2a,

+ Tam giác SAC là tam giác vuông tại S nên ta có:

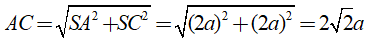
Xét tam giác ABC có: AB² + BC² = AC² =8a²

Suy ra tam giác ABC vuông tại B.

+ Gọi H là trung điểm của AC

=> HA= HB= HC.

Lại có SA= SB= SC ( giả thiết)

Do đó,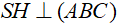

+ Ta có: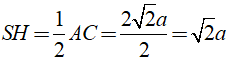

Diện tích tam giác ABC là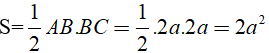

Thể tích hình chóp S. ABC là: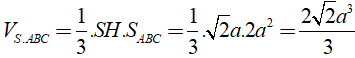

Chọn C.

Ví dụ 2: Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A’ trên cạnh SA sao cho SA'=1/2SA . Mặt phẳng qua A’ và song song với đáy của hình chóp cắt các cạnh SB, SC, SD lần lượt tại B’, C’, D’. Khi đó thể tích khối chóp S.A’B’C’D’ bằng:

A. V/3

B. V/9

C. V/27

D. V/81

Hướng dẫn giải:

Gọi thể tích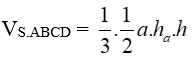

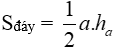
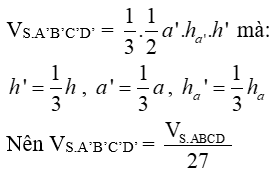
Với h là chiều cao hính chóp S.ABCD

Chọn đáp án C.

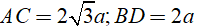
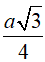
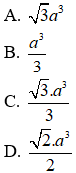
Ví dụ 3 Cho hình chóp S.ABCD có đáy ABCD là hình thoi; hai đường chéo và cắt nhau tại O; hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm O đến mặt phẳng (SAB) bằng . Tính thể tích khối chóp S.ABCD

Hướng dẫn giải

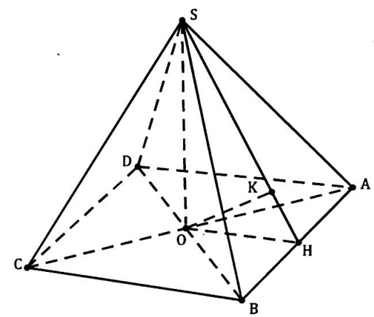
+ Do tam giác ABD đều nên với H là trung điểm của AB, K là trung điểm của HB ta có:

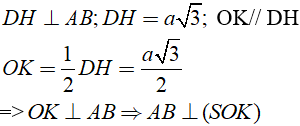
+ Gọi I là hình chiếu của O lên SK ta có:

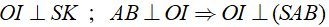
hay OI là khoảng cách từ O đến mặt phẳng (SAB).

Tam giác SOK vuông tại O, OI là đường cao

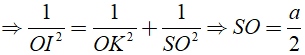
Diện tích đáy SABCD = 4SABO = 2. OA. OB =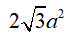

Đường cao của hình chóp là SO=a/2

Thể tích khối chóp S.ABCD: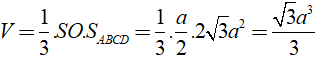

Chọn C.

Ví dụ 4. Cho hình hình chóp S.ABCD có cạnh SA=3/4, tất cả các cạnh còn lại đều bằng 1. Tính thể tích khối chóp S. ABCD

Hướng dẫn giải

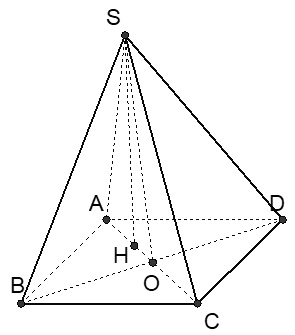
Gọi O là giao điểm của AC và BD

Tam giác SBD cân tại S( SB= SD), có SO là đường trung bình nên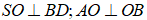

Đặt AC= 2x.

Ta có SO² = SB² – OB² = AB² - OB² = OA² = x²

Áp dụng công thức đường trung tuyến:

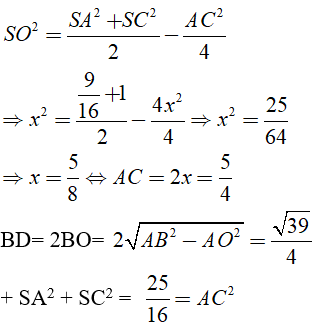
=> Tam giác SAC vuông tại S.

+) Kẻ

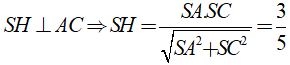
Do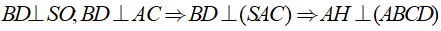

Khi đó, thể tích hình chóp S.ABCD là:

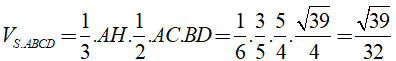
Chọn C.

Ví dụ 5. Cho hình chóp S. ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho 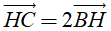hợp với đáy một góc 60^o. Tính thể tích của khối chóp S.ABC

Hướng dẫn giải

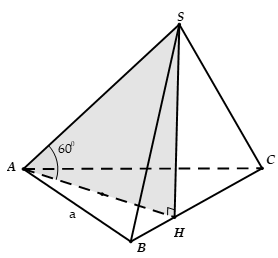
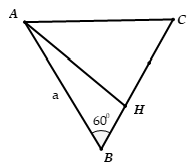
Ta có: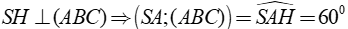

Xét tam giác AHB,áp dụng định lí cosin trong ta có:

AH² = AB² + BH² – 2AB.BH.cos

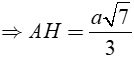
Xét tam giác SAH vuông tại H có:

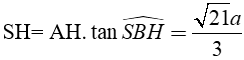
Do tam giác ABC là tam giác đều cạnh a nên diện tích tam giác ABC là: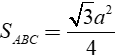

Vậy thể tích hình chóp S. ABC là: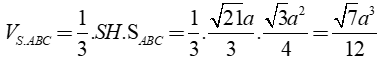

Chọn B.