Phương pháp tính thể tích hình chóp có mặt bên vuông góc với đáy - Toán lớp 12

Phương pháp tính thể tích hình chóp có mặt bên vuông góc với đáy

Với Phương pháp tính thể tích hình chóp có mặt bên vuông góc với đáy Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính thể tích hình chóp có mặt bên vuông góc với đáy từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

* Khối chóp có mặt bên vuông góc với đáy ta suy ra đường cao của mặt bên vuông góc với đáy - là đường cao của chóp hay h = độ dài đường cao hạ từ đỉnh chóp của mặt bên vuông góc với đáy.

2. Ví dụ minh họa

Ví dụ 1. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp S. ABC.

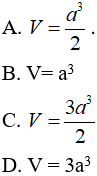
Hướng dẫn giải

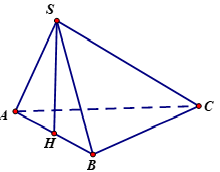
Gọi H là trung điểm của AB.

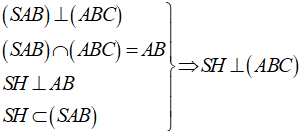
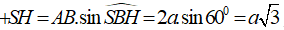
Tam giác ABC đều độ dài cạnh 2a nên diện tích tam giác ABC là:

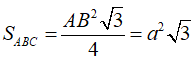
+ Thể tích hình chóp S.ABC là:

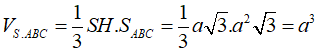
Chọn B.

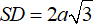
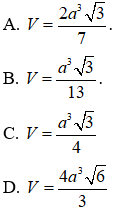
Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD). Biết và góc tạo bởi đường thẳng SC và mặt phẳng (ABCD) bằng 30^o . Tính thể tích V của khối chóp S.ABCD.

Hướng dẫn giải

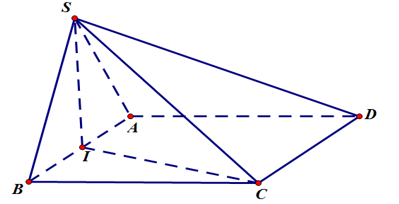
Gọi I là trung điểm AB.

Do tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với (ABCD) nên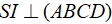

Khi đó, hai tam giác vuông : ∆SIC= ∆SID ( c.g.c)

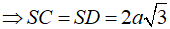
Do góc tạo bởi đường thẳng SC và mặt phẳng (ABCD) bằng 300 nên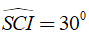

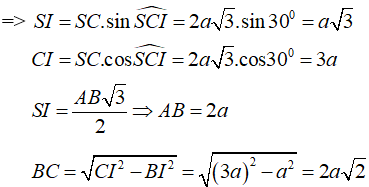
Từ đó, diện tích hình chữ nhật ABCD là :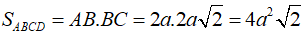

Vậy thể tích hình chóp S.ABCD là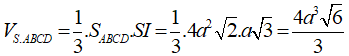

Chọn D

Ví dụ 3. Cho hình chóp S. ABC có SA= a, tam giác ABC đều, tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng

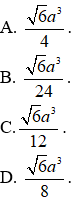
Hướng dẫn giải

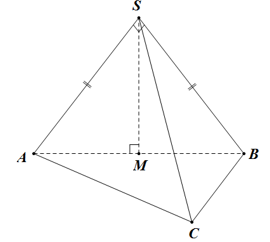
Tam giác SAB vuông cân tại S và SA= a nên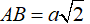

+ Gọi M là trung điểm AB suy ra 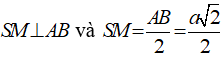(SM là đường trung tuyến của tam giác SAB vuông cân tại S).

Mặt khác:

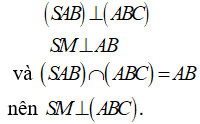
Suy ra SM là đường cao của hình chóp S. ABC ứng với đáy là tam giác ABC.

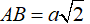
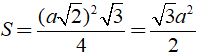
+Tam giác ABC là tam giác đều có độ dài cạnh là nên diện tích tam giác ABC là:

+ Thể tích khối chóp S.ABC là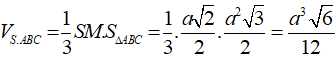

Chọn C.

Ví dụ 4. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, tam giác SAD cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa (SBC) và mặt đáy bằng 60^o . Tính thể tích S.ABCD bằng:

Hướng dẫn giải

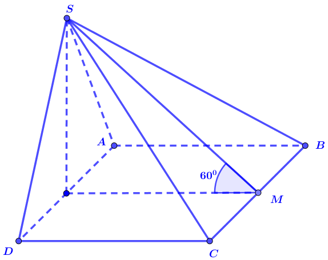
Gọi H là trung điểm AD.

+ Ta có: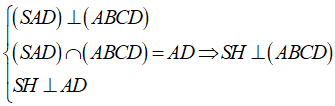

Do ABCD là hình vuông cạnh 2a nên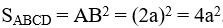

+ Tam giác SBC cân tại S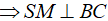

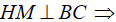
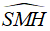
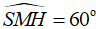
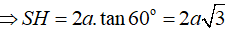
Mà góc giữa mặt phẳng (SBC) và mặt phẳng (ABCD) là góc giữa hai đường thẳng HM và SM chính là góc . Theo bài ra có .

Vậy thể tích S.ABCD: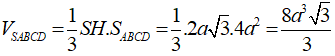

Chọn B.

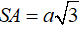
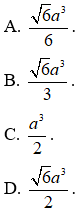
Ví dụ 5. Cho hình chóp S.ABC có đáy ABC là tam giác đều; mặt bên (SAB) nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S,, SB= a. Tính thể tích khối chóp S. ABC.

Hướng dẫn giải

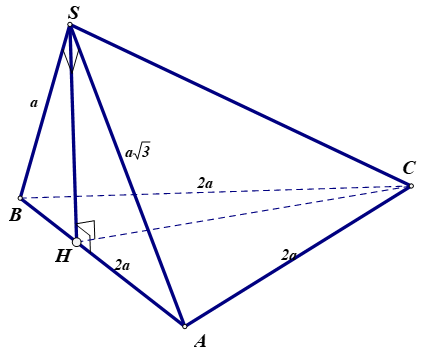
+ Do tam giác SAB vuông tại S nên có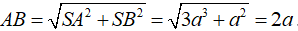

Và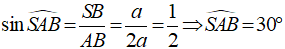

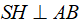
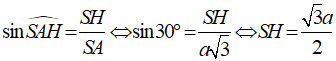
+ Dựng , xét tam giác SAH có

Do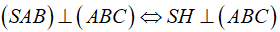

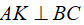
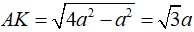
+ Dựng ,do tam giác ABC đều nên AK là trung trực và có

Có

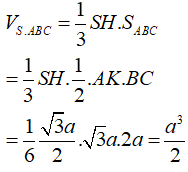
Chọn C.