Phương pháp tính tỉ số thể tích của hai khối chóp cực hay - Toán lớp 12

Phương pháp tính tỉ số thể tích của hai khối chóp cực hay

Với Phương pháp tính tỉ số thể tích của hai khối chóp cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính tỉ số thể tích của hai khối chóp từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

Cho khối chóp S. AB

C. Trên ba đường thẳng SA , SB, SC lần lượt lấy các điểm A’, B’, C’ khác S. Khi đó: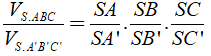

2. Ví dụ minh họa

Ví dụ 1.Cho tam giác ABC vuông cân ở A và AB= a. Trên đường thẳng qua C và vuông góc với (ABC) lấy điểm D sao cho CD= a. Mặt phẳng (α) qua C và vuông góc với BD, cắt BD tại F và cắt AD tại E. Thể tích khối tứ diện CDEF giá trị nào sau đây?

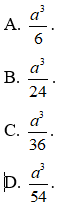
Hướng dẫn giải

+ Ta có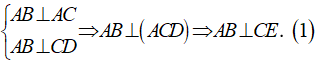

Lại có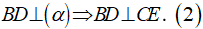

Từ (1) và (2), suy ra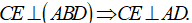

+ Trong tam giác DCB, ta có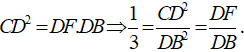

Tương tự, ta cũng có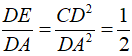

Áp dụng công thức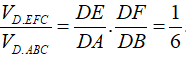

Suy ra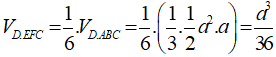

Chọn C.

Ví dụ 2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại đỉnh B, AB= a, SA= 2a và SA vuông góc với mặt phẳng đáy. Gọi H; K lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích khối tứ diện S.AHK.

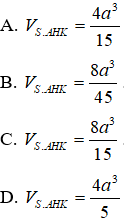
Lời Giải

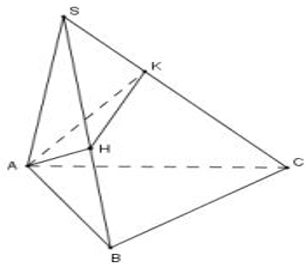
Xét tam giác ABC vuông cân tại B, ta có

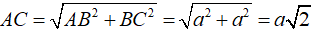
Xét tam giác SAB vuông tại A, ta có

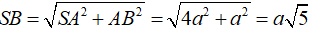
Xét tam giác SAC vuông tại A, ta có:

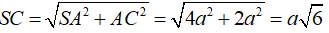
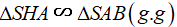
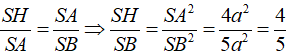
Ta có nên

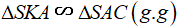
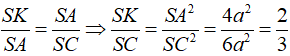
Ta có nên

Thể tích khối chóp S. ABCD là

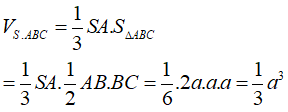
Ta có tỉ số

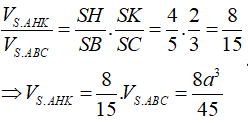
Chọn B.

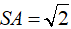
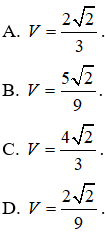
Ví dụ 3. Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và B, BA= BC= 1; AD= 2. Cạnh bên SA vuông góc với đáy và . Gọi H là hình chiếu vuông góc của A trên SB. Tính thể tích của khối đa diện S. AHCD.

Hướng dẫn giải

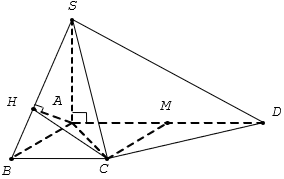
Tam giác vuông SAB, có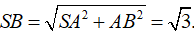

Gọi M là trung điểm AD. Tứ giác ABCM là hình vuông nên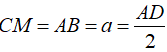

Tam giác ACD có đường trung tuyến CM bằng nửa cạnh tương ứng AD nên tam giác này vuông tại C.

Ta có V_S.AHCD = V_S.ACD + V_S.AHC

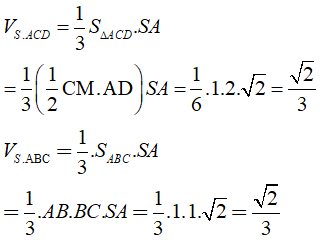
+ Ta có: SH.SB=SA² nên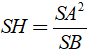

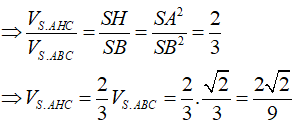
Vậy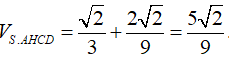

Chọn B.

Ví dụ 4. Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng 2a, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 45^o. Gọi M, N và P lần lượt là trung điểm các cạnh SA, SB và AB. Tính thể tích V của khối tứ diện DMNP.

Hướng dẫn giải

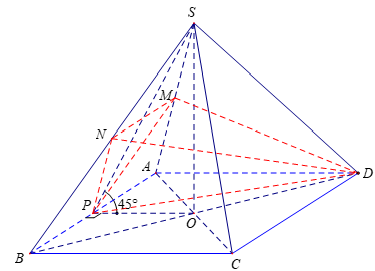
Ta có: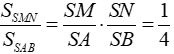

Tương tự,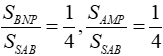

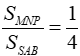
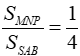
Suy ra (có thể khẳng định nhờ hai tam giác MNP và BAS là hai tam giác đồng dạng với tỉ số k=1/2).

Do đó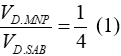

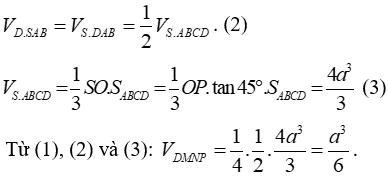
Chọn A.

Ví dụ 5. Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng 2a, góc giữa hai hai mặt phẳng (SAB) và (ABCD) bằng 45^o. Gọi M, N, P lần lượt là trung điểm SA, SB và AB. Tính thể tích V khối tứ diện D.MNP.

Hướng dẫn giải

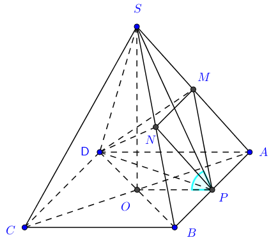
Ta có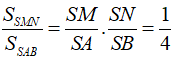

Tương tự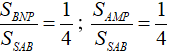

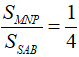
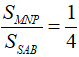
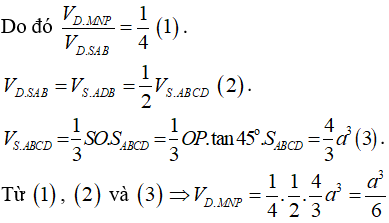
Suy ra ( có thể khẳng định là do hai tam giác MNP và BAS đồng dạng với tỉ số k=1/2).

Chọn A.