Cách xác định mặt cầu cực hay (mặt cầu ngoại tiếp, mặt cầu nội tiếp) - Toán lớp 12

Cách xác định mặt cầu cực hay (mặt cầu ngoại tiếp, mặt cầu nội tiếp)

Với Cách xác định mặt cầu cực hay (mặt cầu ngoại tiếp, mặt cầu nội tiếp) Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập mặt cầu từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

Muốn xác định tâm và bán kính của mặt cầu chúng ra cần dựa vào các tính chất sau đây:

• Tập hợp tất cả những điểm M trong không gian cách điểm O cố định một khoảng bằng R cho trước là mặt cầu tâm O bán kính R.

• Tập hợp tất cả những điểm M nhìn đoạn thẳng AB cố định dưới một góc vuông là mặt cầu đường kính AB.

• Tập hợp tất cả những điểm M sao cho tổng bình phương các khoảng cách tới hai điểm A, B cố định bằng một hằng số k² là mặt cầu có tâm là trung điểm O của đoạn AB và bán kính r = .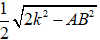

2. Ví dụ minh họa

Ví dụ 1. Cho tứ diện ABCD. Tìm tập hợp tất cả các điểm M trong không gian sao cho
|MA→ + MB→ + MC→ + MD→| = 4 .

A. Mặt nón, bán kính đáy bằng 1.

B. Mặt cầu, bán kính bằng 1.

C. Mặt trụ, bán kính bằng 1.

D. Mặt cầu, bán kính bằng 2.

Hướng dẫn giải:

+ Ta có |MA→ + MB→ + MC→ + MD→| = 4
⇔ |4MG→| = 4 ⇔ MG = 1

(với G là trọng tâm tứ diện ABCD).

+ Vậy tập hợp các điểm M trong không gian thỏa mãn là mặt cầu tâm G bán kính R= 1.

Chọn B.

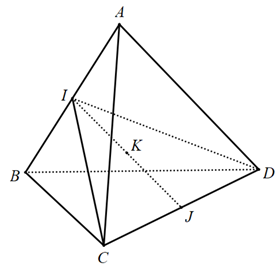
Ví dụ 2. Cho tứ diện đều ABCD có cạnh bằng a. Tìm tập hợp các điểm M trong khôn gian sao cho:
MA² + MB² + MC² + MD² ≤ 2a² (*)

A. Mặt trụ, bán kính bằng .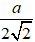

B. Mặt cầu, bán kính bằng .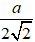

C. Khối trụ, bán kính bằng .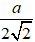

D. Khối cầu, bán kính bằng .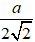

Hướng dẫn giải:

Gọi I là trung điểm của cạnh AB, J là trung điểm của CD, K là trung điểm IJ.

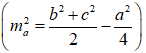
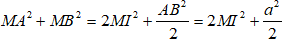
Áp dụng định lý trung tuyến trong tam giác ta có:

.

Suy ra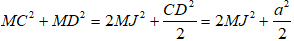

MA² + MB² + MC² + MD² = 2(MI² + MJ²) + a²
=

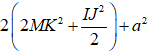
Ta có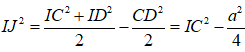
=

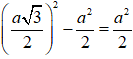
Suy ra MA² + MB² + MC² + MD² = 4MK² +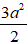

Do đó:
(*) ⇔
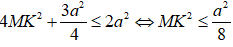
⇔ MK ≤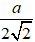

Vậy tập hợp các điểm M trong không gian là khối cầu tâm K bán kính R =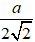

Chọn D.

Ví dụ 3. Cho mặt cầu S_{(O; R)} và điểm A cố định với OA = d. Qua A, kẻ đường thẳng Δ tiếp xúc với mặt cầu S_{(O; R)} tại M. Công thức nào sau đây được dùng để tính độ dài đoạn thẳng AM?

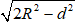
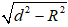
A.    B.

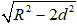
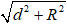
C.    D.

Hướng dẫn giải:

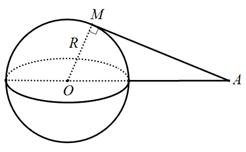
Vì Δ tiếp xúc với S_{(O; R)} tại M nên OM ⊥ Δ tại M.

Xét tam giác OMA vuông tại M, ta có:

AM² = OA² - OM² = d² - R²
⇒ AM =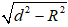

Chọn B

Ví dụ 4. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết SA ⊥ (ABC) , AB = a,
= 30⁰ , góc giữa (SBC) và (ABC) bằng 60⁰. Xét vị trí tương đối giữa mặt cầu S_{(A; a)} và mặt phẳng ( SBC).

A. Mặt phẳng ( SBC) tiếp xúc mặt cầu S_(A,a).

B. Mặt phẳng ( SBC) không cắt mặt cầu S_{(A; a)}.

C. Mặt phẳng ( SBC) cắt mặt cầu S_(A;a) theo đường tròn lớn.

D. Mặt phẳng (SBC) cắt mặt cầu S_{(A; a)} theo giao tuyến là một đường tròn.

Hướng dẫn giải:

Ta có: = 60⁰ ⇒ SA = a√3

Gọi H là hình chiếu của A trên SB, ta chứng minh được AH = d(A, (SBC)) .

Ta có: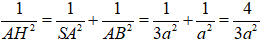

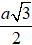
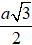
⇒ AH = ⇒ d(A, (SBC)) = AH = < a = R

Vậy mặt phẳng (SBC) cắt mặt cầu S_(A;a) theo giao tuyến là một đường tròn.

Chọn D.

Ví dụ 5. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết SA ⊥ (ABC) , AB= a,
= 30⁰ , góc giữa (SBC) và (ABC) bằng 60⁰. Mặt cầu S_(A;a) cắt mặt phẳng (SBC) theo giao tuyến là một đường tròn (C). Tính bán kính của (C).

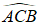
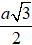
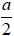
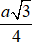
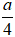
A. r =    B. r =    C. r =    D. r =

Hướng dẫn giải:

Ta có: 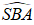= 60⁰ ⇒ SA = a√3

Gọi H là hình chiếu của A trên SB, ta chứng minh được AH = d(A; (SBC)).

Ta có: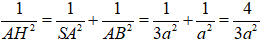

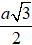
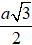
⇒ AH = ⇒ d(A, (SBC)) = AH = < a = R

Vậy mặt phẳng (SBC) cắt mặt cầu S_{(A; a)} theo giao tuyến là một đường tròn có bán kính

r =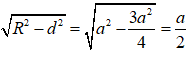

Chọn B.