Cách xác định mặt cầu nội tiếp, ngoại tiếp lăng trụ cực hay - Toán lớp 12

Cách xác định mặt cầu nội tiếp, ngoại tiếp lăng trụ cực hay

Với Cách xác định mặt cầu nội tiếp, ngoại tiếp lăng trụ cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập mặt cầu nội tiếp, ngoại tiếp lăng trụ từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

a.Mặt cầu ngoại tiếp lăng trụ

+ Để một hình lăng trụ có mặt cầu ngoại tiếp thì hình lăng trụ đó phải là hình lăng trụ đứng và có đáy lăng trụ là một đa giác nội tiếp một đường tròn.

+ Gọi O₁, O₂ lần lượt là tâm đường tròn ngoại tiếp hai đáy lăng trụ

⇒ O₁O₂ là trục đường tròn ngoại tiếp hai đa giác đáy.

Gọi I là trung điểm của O₁O₂
⇒ IA = IB = IC= IA’ = IB’ = IC’. Suy ra:

- Trung điểm I của O₁O₂ là tâm mặt cầu ngoại tiếp lăng trụ.

- Bán kính: R = IA
=

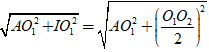
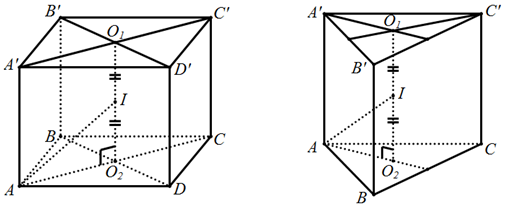
Phương pháp riêng cho hình lập phương và hình hộp chữ nhật:

-Tâm đường tròn ngoại tiếp chính là trung điểm của một đường chéo của hình hộp (giao các đường chéo).

- Bán kính
R =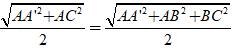

b. Mặt cầu nội tiếp lăng trụ

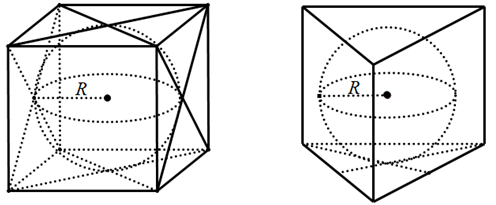
- Khối cầu nội tiếp hình lập phương cạnh a: bán kính R =

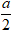
- Đường cao của hình lăng trụ bằng đường kính của hình cầu nội tiếp.

2. Ví dụ minh họa

Ví dụ 1. Cho hình hộp chữ nhật ABCD. A’B’C’D’ nội tiếp trong mặt cầu bán kính R = 3cm. Tam giác ABC cân và có diện tích bằng 2cm. Diện tích toàn phần của hình hộp đó bằng:

A. 8cm²    B. 24cm²

C. 8√7cm²    D. 8(1 + 2√7) cm²

Hướng dẫn giải:

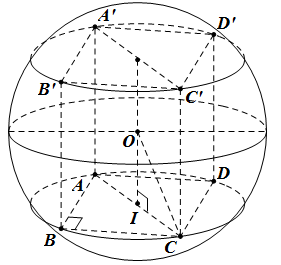
+ Ta có ABCD là hình chữ nhật nên tam giác ABC vuông tại B.

Theo giả thiết tam giác ABC cân nên tam giác ABC vuông cân tại B ⇒ AB= BC

+ Diện tích tam giác ABC là
S_ABC = .AB.BC = = AB² = 2
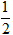
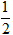
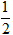
⇒ AB = BC = 2

Tam giác ABC có: AC = 2√2 ⇒ IC = AC/2 = √2

Xét tam giác IOC:
IO = 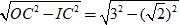= √7

+ Suy ra chiều cao của khối hộp là

+ Diện tích toàn phần của hình hộp ABCD.A’B’C’D’ là: S_tp = S_{2 đay} + S_xq

= 2.2² + 4.2.2√7 = 8 + 16√7 = 8(1 + 2√7)

Chọn D.

Ví dụ 2. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại C, AC = a,
BC = a√2 . Góc giữa đường chéo AC’ của mặt bên (A’C’CA) với mặt đáy bằng 30⁰. Tính thể tích khối cầu ngoại tiếp hình lăng trụ.

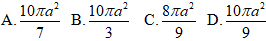
Hướng dẫn giải:

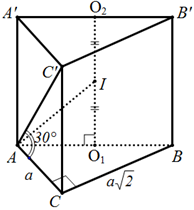
Gọi O₁, O₂ lần lượt là tâm đường tròn ngoại tiếp hai đáy.

+ Vì tam giác ABC vuông tại C nên tâm đường tròn ngoại tiếp tam giác là O₁ – trung điểm của cạnh huyền AB.

Tương tự ta có, tâm đường tròn ngoại tiếp tam giác A’B’C’ là O₂ – trung điểm của cạnh huyền A’B’.

Gọi I là trung điểm của O₁O₂ là tâm mặt cầu ngoại tiếp lăng trụ, bán kính mặt cầu là IA.

+ Xác định góc của đường AC’ và (ABC):

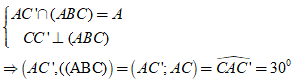
+ Xét tam giác ACC’:

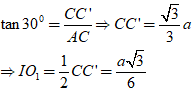
+ Xét tam giác ABC có:

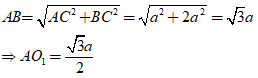
+ xét tam giác AIO₁ có:

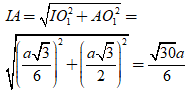
Thể tích khối cầu là:
V =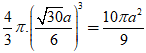

Chọn D.

Ví dụ 3. Một khối cầu nội tiếp trong hình lập phương có chu vi đáy là 4cm. Diện tích của mặt cầu là:

A. S = 2π    B. S = 4π
C. S = 3π    D. S = π

Hướng dẫn giải:

Gọi độ dài cạnh hình lập phương là a.

Chu vi đáy của hình lập phương là P = 4a = 4 cm

⇒ độ dài một cạnh là a = 1 cm

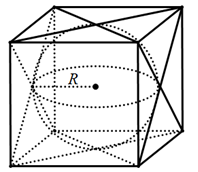
Bán kính hình cầu nội tiếp lập phương là
r = = cm

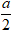
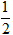
Diện tích của mặt cầu là: S = 4π(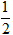)² cm²

Chọn D

Ví dụ 4. Xét một hộp bóng bàn có dạng hình hộp chữ nhật. Biết rằng hộp chứa vừa khít ba quả bóng bàn được xếp theo chiều dọc, các quả bóng bàn có kích thước như nhau. Phần không gian còn trống trong hộp chiếm bao nhiêu % của chiếc hộp.

A. 65, 09%.    B. 47,64%.    C. 82,55 %.    D. 83,3%.

Hướng dẫn giải:

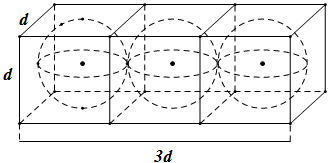
Gọi đường kính quả bóng bàn là d. Khi đó kích thước của hình hộp chữ nhật là d; d; 3d.

Bán kính của mỗi quả bóng là r =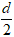

Thể tích của hình hộp chữ nhật là:
V₁ = d.d.3d = 3d³.

Thể tích của ba quả bóng bàn là

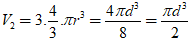
Thể tích của phần không gian còn trống trong hộp là:
V₃ = V₁ - V₂ = 3d³ -

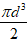
Phần không gian còn trống trong hộp chiếm:

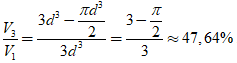
Chọn B.

Ví dụ 5. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi R₁, R₂, R₃ lần lượt là bán kính mặt cầu ngoại tiếp hình lập phương, bán kính mặt cầu nội tiếp hình lập phương và bán kính mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương. Khẳng định nào sau đây đúng?

A. R₂² = R₁.R₃    B. R₂² = R₁² + R₃²

C. R₁² = R₂² + R₃²    D. R₃² = R₁.R₂ .

Hướng dẫn giải:

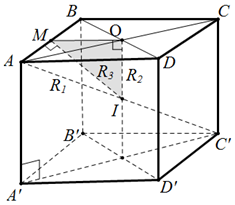
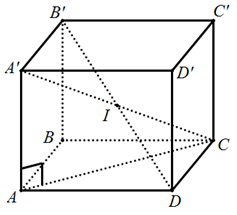
Gọi O là tâm hình vuông ABCD, gọi M là trung điểm của AB và I là trung điểm của AC’.

Khi đó, bán kính mặt cầu ngoại tiếp hình lập phương là :
R₁ = IA =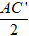

Bán kính mặt cầu nội tiếp hình lập phương là : R₂ = IO

Bán kính mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương là : R₃ = IM

Ta có R₁, R₂, R₃ như trên hình vẽ.

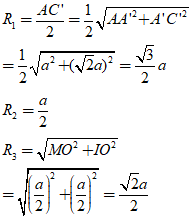
Kiểm tra ta thấy: R₁² = R₂² + R₃²

Chọn C.