Số phức z thỏa mãn điều nào thì có điểm biểu diễn thuộc phần gạch chéo
Câu hỏi:
Số phức z thỏa mãn điều nào thì có điểm biểu diễn thuộc phần gạch chéo như trên hình.
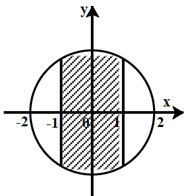
A. Số phức z = a + bi; |z| ≤ 2; -1 ≤ a ≤ 1.
B. Số phức z = a + bi; |z| ≤ 2; a < -1; a > 1.
C. Số phức z = a + bi; |z| < 2; -1 ≤ a ≤ 1.
D. Số phức z = a + bi; |z| ≤ 2; -1 ≤ b ≤ 1.
Trả lời:
Chọn A.
+ Từ hình biểu diễn ta thấy tập hợp các điểm M(a; b) biểu diễn số phức z trong phần gạch chéo đều thuộc đường tròn tâm O(0;0) và bán kính bằng 2; ngoài ra -1 ≤ a ≤ 1.
+ Vậy M(a; b) là điểm biểu diễn của các số phức z = a + bi có mô đun nhỏ hơn hoặc bằng 2 và có phần thực thuộc đoạn [-1;1].
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hai số phức z1; z2 khác 0 thỏa mãn .Gọi A; B lần lượt là các điểm biểu diễn cho số phức z1; z2. Khi đó tam giác OAB là:
Xem lời giải »
Câu 2:
Cho số phức z thỏa mãn . Giá trị của |z| là ?
Xem lời giải »
Câu 4:
Số nghiệm của phương trình với ẩn số phức z: 4z2 + 8|z|2 - 3 = 0 là:
Xem lời giải »
Câu 5:
Trong mặt phẳng phức Oxy, số phức z thỏa điều kiện nào thì có điểm biểu diễn số phức thuộc phần tô màu như hình vẽ
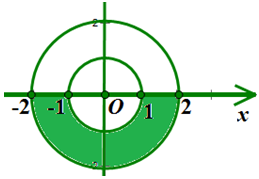
Xem lời giải »
Câu 6:
Cho số phức z thỏa mãn |z – 4| + |z + 4| = 10. Giá trị lớn nhất và nhỏ nhất của mô – đun của số phức z là
Xem lời giải »
Câu 7:
Gọi (H) là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy để 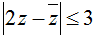 với số phức z có phần thực không âm. Tính diện tích hình (H).
với số phức z có phần thực không âm. Tính diện tích hình (H).
Xem lời giải »
Câu 8:
Có số phức z có phần ảo bằng 164 và n ∈ R* thỏa mãn: 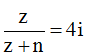 . Tìm n?
. Tìm n?
Xem lời giải »



