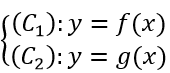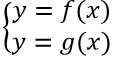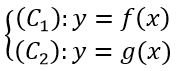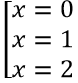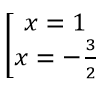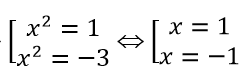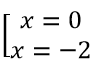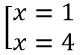Cách tìm giao điểm của đồ thị hàm số cực hay - Toán lớp 12

Cách tìm giao điểm của đồ thị hàm số cực hay

Với Cách tìm giao điểm của đồ thị hàm số cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm giao điểm của đồ thị hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

1. Bài toán tổng quát

Trong mặt phẳng (Oxy) hãy xét sự tương giao của đồ thị hàm số

Cho hàm số y = f(x) có đồ thị là (C₁) và hàm số y=g(x) có đồ thị là (C₂). Khi đó nếu M(x; y) là giao điểm của (C₁) và (C₂) thì tọa độ của M là nghiệm của hệ phương trình:

Phương trình (*)

f(x) = g(x)

được gọi là phương trình hoành độ giao điểm của hai đồ thị (C₁) và (C₂)

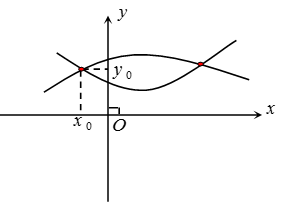
Nghiệm x_o của phương trình (*) chính là hoành độ điểm chung của (C₁) và (C₂)

Khi đó tung độ điểm chung là y_o = f(x_o) hoặc y_o=g(x_o)

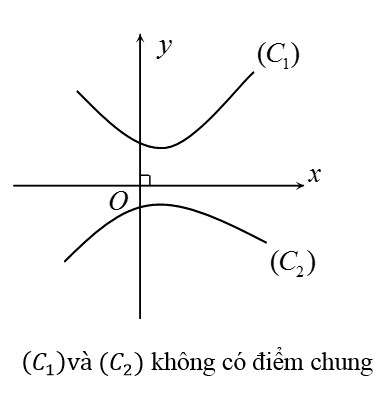
Nếu (*) vô nghiệm thì (C₁) và (C₂) không có điểm chung

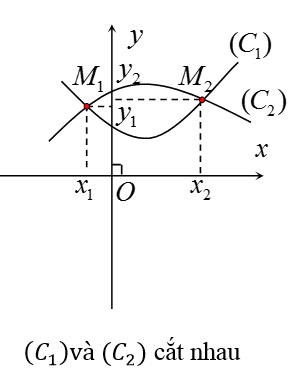
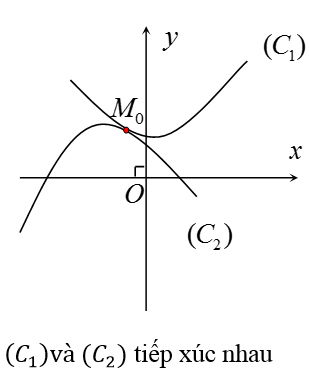
Nếu (*) có n nghiệm thì (C₁) và (C₂) có n điểm chung

2. Phương pháp chung

Để giải một bài toán về tính chất giao điểm của hai đồ thị (C₁) và (C₂) ta có thể tiến hành theo các bước sau:

Lập phương trình hoành độ giao điểm của hai đồ thị (C₁) và (C₂) (tức phương trình (*))

Biến đổi phương trình này về dạng đơn giản hơn( thường thì sau khi biến đổi ta sẽ thu được phương trình bậc hai, bậc ba hoặc phương trình trùng phương…)

Dựa vào điều kiện của bài toán ban đầu, ta đưa về điều kiện cho phương trình vừa biến đổi.

3. Bài toán tìm giao điểm của hai đồ thị hàm số

Bài toán: Tìm tọa độ giao điểm của hai đồ thị hàm số

    Bước 1: Lập phương trình hoành độ giao điểm: f(x) = g(x) (1)

    Bước 2: Giải phương trình (1) tìm x ⇒ y

    Bước 3: Kết luận số giao điểm của (C₁) và (C₂) chính là số nghiệm của (1)

Ví dụ minh họa

Ví dụ 1: Tìm giao điểm của đồ thị hàm số (C): y = x³ - 3x² + 2x + 1 và đường thẳng y = 1

   Hướng dẫn:

Phương trình hoành độ giao điểm x³ - 3x² + 2x + 1 = 1

⇔ x³ -3x² + 2x = 0 ⇔

Với x = 0 ⇒ y = 1

Với x = 1 ⇒ y = 1

Với x = 2 ⇒ y = 1

   Vậy tọa độ giao điểm cần tìm là (0; 1); (1; 1) và (2; 1)

Ví dụ 2: Tìm tọa độ giao điểm giữa đồ thị y= (2x + 1)/(2x - 1) và đường thẳng d: y = x + 2

   Hướng dẫn

Phương trình hoành đô giao điểm (2x + 1)/(2x - 1) = x + 2 (1)

Điều kiện x ≠ 1/2

Khi đó (1) ⇔ 2x + 1 = (2x - 1)(x + 2) ⇔ 2x² + x - 3 = 0 ⇔

Với x = 1 ⇒ y = 3

Với x = -3/2 ⇒ y = 1/2

   Vậy tọa độ giao điểm cần tìm là (1; 3) và (-3/2; 1/2)

Ví dụ 3: Tìm giao điểm của đồ thị hàm số (C): y = x⁴ + 2x² - 3 và trục hoành

   Hướng dẫn

Phương trình hoành độ giao điểm x⁴ + 2x² - 3 = 0 ⇔

   Vậy tọa độ giao điểm cần tìm là A(-1; 0), B(1; 0)

B. Bài tập vận dụng

Câu 1: Tìm tọa độ giao điểm của hai đường cong (C₁ ):y = x² -4 và (C₂): y = -x² - 2x

Lời giải:

Phương trình hoành độ giao điểm x² - 4 = -x² - 2x ⇔ 2x² + 2x - 4 ⇔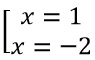

   Vậy tọa độ giao điểm cần tìm là A(1; -3), B(-2 ;0)

Câu 3: Tìm tọa độ giao điểm của hai đường cong (C₁ ):y = (2x - 1)/(x + 1) và (C₂): y = -3x - 1

Lời giải:

ĐKXĐ x ≠ -1

Phương trình hoành độ giao điểm (2x - 1)/(x + 1) = -3x - 1 ⇒ 3x² + 6x = 0 ⇔

   Vậy tọa độ giao điểm cần tìm là A(0; -1), B(-2; 5)

Câu 4: Tìm tọa độ giao điểm của hai đường cong (C₁ ):y =√x và (C₂):y=x-2

Lời giải:

ĐKXĐ x ≥ 0

Phương trình hoành độ giao điểm √x = x - 2 ⇔ x² - 5x + 4 ⇔

   Vậy tọa độ giao điểm cần tìm là A(1; -1), B(4; 2)

Câu 5: Gọi M, N là hai giao điểm của đường thẳng d: y = x + 1 và (C):y = (2x+4)/(x-1). Tìm tọa độ trung điểm I của MN

Lời giải:

ĐKXĐ x ≠ 1

Phương trình hoành độ giao điểm (2x + 4)/(x - 1) = x + 1 ⇔ x² - 2x - 5

Theo Viet có x₁ + x₂ = 2 ⇒ (x₁ + x₂)/2 = 1⇒ x_I = 1⇒ y_I = 2

   Vậy tọa độ giao điểm cần tìm là I(1; 2)

Câu 6: Biết tiệm cận ngang của đồ thị hàm số (H):y = (x + 2)/(x + 1) và (C):y = 2x⁴ - x² cắt nhau tại I. Tìm tọa độ giao điểm I.

Lời giải:

Tiệm cận ngang của đồ thị hàm số (H): y = 1

Phương trình hoành độ giao điểm 2x⁴ - x² -1 = 0 ⇔

   Vậy tọa độ giao điểm cần tìm là (1; 1),(-1; 1)

Câu 7: Tìm tọa độ giao điểm giữa đồ thị hàm số (C);y = (x² - 2x - 3)/(x - 1) và đường thẳng d: y = x + 1

Lời giải:

ĐKXĐ x ≠ 1

Phương trình hoành độ giao điểm (x² - 2x - 3)/(x - 1) = x + 1⇔ 2x + 2 = 0⇔ x = -1

   Vậy tọa độ giao điểm cần tìm là (-1; 0)

Câu 8: Tìm số giao điểm của đồ thị hàm số y = x⁴ - 4x² - 2 có đồ thị (C) và đồ thị (P): y = 1 - x²

Lời giải:

Phương trình hoành độ giao điểm x⁴ - 3x² - 3 = 0

Phương trình có S > 0;P < 0 nên phương trình có một nghiệm dương

   Số giao điểm cần tìm là 2