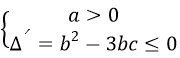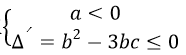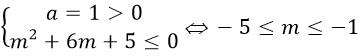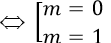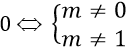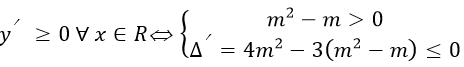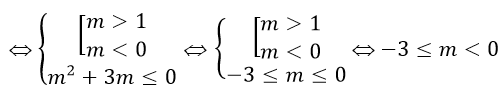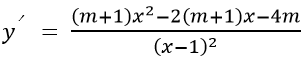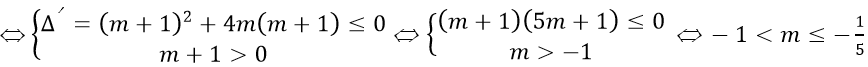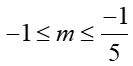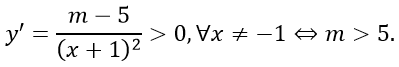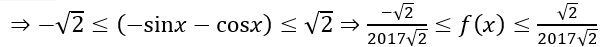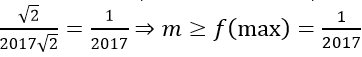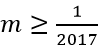Tìm tham số m để hàm số đơn điệu cực hay - Toán lớp 12

---

Tìm tham số m để hàm số đơn điệu cực hay

Với Tìm tham số m để hàm số đơn điệu cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm tham số m để hàm số đơn điệu từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

Phương pháp giải

1. Hàm đa thức bậc ba: y=f(x)=ax³+bx²+cx+d (a≠0)

⇒ f'(x)=3ax²+2bx+c

    Hàm đa thức bậc ba y=f(x) đồng biến trên R khi và chỉ khi

   Hàm đa thức bậc ba y=f(x) nghịch biến trên R khi và chỉ khi

2. Hàm phân thức bậc nhất: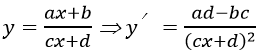

    Hàm số đồng biến trên các khoảng xác định khi y'>0 hay ad-bc>0

   Hàm số nghịch biến trên các khoảng xác định khi y'>0 hay ad-bc<0

Ví dụ minh họa

Ví dụ 1: Cho hàm số 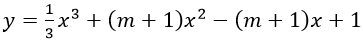đồng biến trên tập xác định.

Hướng dẫn

      + Tập xác định: D=R

      + Ta có: y'=x²+2(m+1)x-(m+1)

      + Δ'=(m+1)²+4(m+1)=m²+6m+5

      + Để hàm số đồng biến trên tập xác định thì

   Vậy giá trị của tham số cần tìm là -5≤m≤-1

Ví dụ 2: Cho hàm số 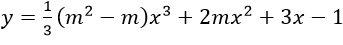. Tìm giá trị của m để hàm số luôn đồng biến trên R.

Hướng dẫn

      + Tập xác định: D=R

      + Đạo hàm y'≠(m²-m) x²+4mx+3

      + Hàm số luôn đồng biến trên R 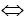y'≥0 ∀ x∈R

    Xét m²-m=0 ⇒

   Với m=0 phương trình trở thành y=3x-1;y'=3>0 ∀x∈R

⇒ m=0 thỏa mãn yêu cầu bài toán.

    Với m=1 phương trình trở thành y=2x²+3x-1;y'=4x+3

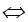
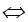
    Khi đó y'>0 4x+3>0 x<-3/4

⇒ m=1 không thỏa mãn yêu cầu bài toán.

    Xét m²-m≠0

   Khi đó

   Từ hai trường hợp trên ta có giá trị m cần tìm là -3≤m<0

Ví dụ 3: Cho hàm số 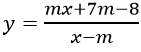. Tìm m để hàm số đồng biến trên từng khoảng xác định.

Hướng dẫn

      + Tập xác định: D=R\{m}

      + Đạo hàm 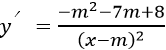. Dấu của y' là dấu của biểu thức -m²-7m+8

      + Hàm số đồng biến trên từng khoảng xác định y'>0 ∀x∈D

-m²-7m+8>0 -8<m<1

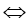
    Vậy giá trị m cần tìm là -8<m<1

B. Bài tập vận dụng

Câu 1: Tìm tất cả các giá trị thực của tham số m để hàm số y = x³ + 3x² + mx + 2 đồng biến trên R.

Lời giải:

+ Ta có: y '= 3x² + 6x + m

      + Để hàm số đã cho đồng biến trên R thì y' ≥ 0,∀x ∈R

      + Yêu cầu bài toán trở thành tìm điều kiện của m để y' ≥ 0,∀x ∈R

Ta có y' = 3x² + 6x + m, ta có: a = 3>0,Δ = 36 - 12m

Để y' ≥ 0,∀x ∈ R khi Δ ≤ 0 ⇔ 36 - 12m ≤ 0 ⇔ m ≥ 3

Vậy giá trị của tham số m cần tìm là m ≥ 3

Câu 2: Tìm tập hợp tất cả các tham số thực của m để hàm số y = x³ - (m + 1) x²+3x+1 đồng biến trên khoảng (-∞;+∞).

Lời giải:

+ Tập xác định D = R.

      + Ta có y' = 3x² - 2(m + 1)x + 3.

      + Hàm số y = x³ - (m + 1) x² + 3x + 1 đồng biến trên khoảng (-∞; +∞)

   ⇔ y' ≥ 0,∀x∈R

    ⇔ Δ' ≤ 0 ⇔ (m + 1)² - 9 ≤ 0 ⇔ m² + 2m - 8 ≤ 0 ⇔ -4 ≤ m ≤2.

Vậy giá trị của tham số m cần tìm là -4 ≤ m ≤ 2

Câu 3: Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y = 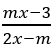đồng biến trên từng khoảng xác định.

Lời giải:

Ta có: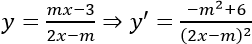

Theo yêu cầu bài toán, để hàm số đồng biến trên từng khoảng xác định thì

y'>0,∀ x ∈D ⇔ -m² + 6 > 0 ⇔ -√6<m<√6

Vậy giá trị của tham số m cần tìm là -√6 < m < √6

Câu 4: Cho hàm số y=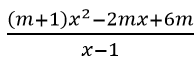. Tìm các giá trị của tham số m để hàm số đồng biến trên mỗi khoảng xác định của nó.

Lời giải:

TXĐ: D = R\{1}

      + Trường hợp 1: Khi m = -1, hàm số trở thành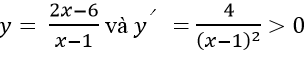 với mọix∈D

Do đó hàm số đồng biến trên mỗi khoảng xác định

⇒ m = -1 thỏa mãn yêu cầu bài toán

      + Trường hợp 2: Khi m ≠ -1, ta có

Đặt g(x) = (m + 1) x² - 2(m + 1)x - 4m và ta có y' cùng dấu với g(x)

Hàm số đồng biến trên mỗi khoảng xác định

    ⇔ ∀ x ∈ D,y' ≥ 0 ⇔ ∀ x ∈D,g(x)≥0

Kết hợp cả 2 trường hợp, vậy tập hợp các giá trị của tham số m thỏa mãn yêu cầu bài toán là

Câu 5: Xác định giá trị của tham số m để hàm số y = (mx + 5)/(x + 1)đồng biến trên từng khoảng xác định.

Lời giải:

Ta có:y'= 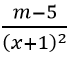. Để hàm số đồng biến trên từng khoảng xác định thì

Vậy giá trị của tham số m cần tìm là m > 5

Câu 6: Tìm giá trị của m để hàm số y = sin⁡x - mx nghịch biến trên R

Lời giải:

Ta có y' = cos⁡x - m.

Để hàm số nghịch biến trên R thì

y' ≤ 0 ∀ x ∈R ⇔ cosx - m ≤ 0 ∀ x ∈ R ⇔ cosx ≤ m ∀x∈R

Vì -1 ≤ cos⁡ x ≤ 1 nên để cosx ≤ m ∀x∈R thì m ≥ 1.

Câu 7: Cho m, n không đồng thời bằng 0. Tìm điều kiện của m, n để hàm số y = msinx - ncosx - 3x nghịch biến trên R.

Lời giải:

Ta có:

y' ≤ 0,∀x ∈ R ⇔ mcosx + nsinx - 3 ≤ 0,∀ x ∈ R ⇔√(m² + n² ) cos(x - α) ≤ 3,∀x∈R

Vậy để hàm số nghịch biến trên R thì m²+n²≤9

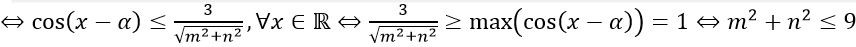
Câu 8: Tìm tham số m thì hàm số y = sinx - cosx + 2017√2 mx đồng biến trên R.

Lời giải:

Tính đạo hàm y' = cosx + sinx + 2017√2 m. y' ≥ 0 ⇔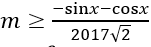=f(x)

Theo bất đẳng thức Bunhiacopxki thì (-sinx - cosx)² ≤ ((-1)² + (-1)² )(sin² x + cos² x) = 2

f(x) đạt giá trị lớn nhất là

Vậy giá trị của tham số m cần tìm là