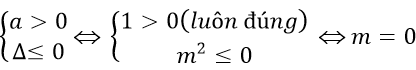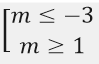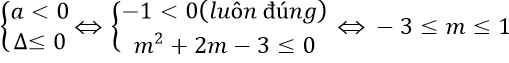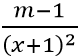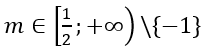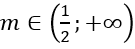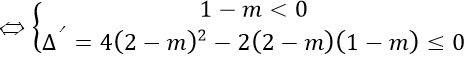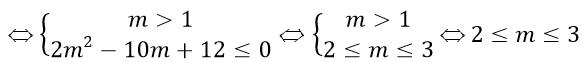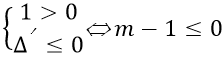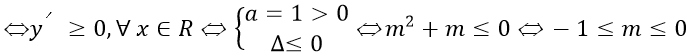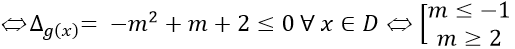Bài tập trắc nghiệm Tìm tham số m để hàm số đơn điệu cực hay - Toán lớp 12

---

Bài tập trắc nghiệm Tìm tham số m để hàm số đơn điệu cực hay

Với Bài tập trắc nghiệm Tìm tham số m để hàm số đơn điệu cực hay Toán lớp 12 tổng hợp 12 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm tham số m để hàm số đơn điệu từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Câu 1: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = 2x³ - 3(m + 2)x² + 6(m + 1)x - 3m + 5 luôn đồng biến trên R.

   A. m = 0

   B. m = -1

   C. m = 2

   D. m = 1

Lời giải:

Đáp án: A

Giải thích :

Ta có y' = 6x² - 6(m + 2)x + 6(m + 1) = 6[x² - (m + 2)x + (m + 1)]

Δ = (m + 2)² - 4(m + 1) = m²

Để hàm số luôn đồng biến trên R thì

.

Câu 2: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y=-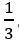 x³-mx²+(2m-3)x-m+2 luôn nghịch biến trên R.

   A. -3 ≤ m ≤1     B. m ≤ 1     C. -3 < m < 1     D.

Lời giải:

Đáp án: A

Giải thích :

Ta có y' = -x² - 2mx + (2m - 3)

Δ' = m² + 2m - 3

Để hàm số luôn nghịch biến trên R thì

.

Câu 3: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y= 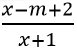nghịch biến trên các khoảng mà nó xác định.

   A. m < -3

   B. m ≤ -3

   C. m ≤ 1

   D. m < 1

Lời giải:

Đáp án: D

Giải thích :

Ta có y'=

Để hàm số nghịch biến trên các khoảng mà nó xác định thì m - 1 < 0

m<1

Câu 4: Tìm số nguyên m nhỏ nhất sao cho hàm số y = 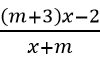luôn nghịch biến trên các khoảng xác định của nó.

   A. m = -1

   B. m = -2

   C. m = 0

   D. Không tồn tại giá trị của m.

Lời giải:

Đáp án: D

Giải thích :

Ta có y'= (m(m + 3) + 2)/(x + 1)² = (m² + 3m + 2)/(x + 1)²

Để hàm số nghịch biến trên các khoảng mà nó xác định thì

m² + 3m + 2 < 0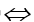 -2<m<-1. Không có giá trị nguyên của m thỏa mãn.

Câu 5: Tìm giá trị của tham số m để hàm số y = 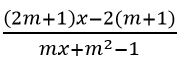đồng biến trên từng khoảng xác định của nó.

    A.

   B.

   C.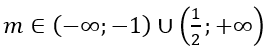

   D.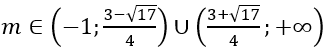

Lời giải:

Đáp án: B

Giải thích :

Ta có y' =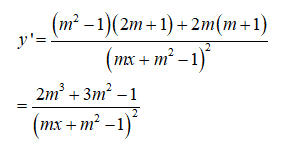

Để hàm số đồng biến trên các khoảng mà nó xác định thì

2m³ + 3m² - 1 > 0 ⇔ (m+1)²(2m-1) > 0 ⇔ 2m - 1 > 0 ⇔ m > 1/2.

Câu 6: (THPT Bình Mỹ - An Giang 2017). Hàm số y=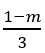 x³-2(2-m) x²+2(2-m)x+5 luôn nghịch biến khi

   A. 2 ≤ m ≤ 3

   B. m = 1

   C. 2 < m < 5

   D. m > -2

Lời giải:

Đáp án: A

Giải thích :

Đạo hàm y' = (1 - m)x² - 4(2 - m)x + 2(2 - m)

Hàm số luôn nghịch biến trên R 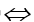y' ≤ 0 ∀ x ∈ R

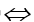
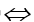
Xét 1 - m = 0 m=1, ta có y'=-4x+2;y'<0 x > 1/2

⇒ m = 1 không thỏa mãn yêu cầu bài toán.

Xét 1 - m ≠ 0

m ≠1

Khi đó y'≤0 ∀ x∈R

Từ hai trường hợp trên ta có giá trị m cần tìm là 2≤m≤3.

Câu 7: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 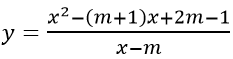đồng biến trên từng khoảng xác định của nó.

   A. m > 1

   B. m ≤ 1

   C. m < 1

   D. m ≥ 1

Lời giải:

Đáp án: B

Giải thích :

Tập xác định D = R\{m}. Ta có y' = (x² - 2mx + m²-m + 1)/(x - m)^2>

Để hàm số tăng trên từng khoảng xác định của nó thì

y' ≥ 0 ∀ x ∈ D ⇔ x² - 2mx + m² - m + 1 ≥ 0 ∀ x ∈ D ⇔

⇔m≤1

Câu 8: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = f(x) = x + m.cos⁡x luôn đồng biến trên R.

   A. |m| ≤ 1     B. m > √3/2     C. |m| ≥ 1     D. m < 1/2

Lời giải:

Đáp án: A

Giải thích :

Tập xác định: D = R. Ta có y' = 1 - msinx

Hàm số đồng biến trên R y' ≥ 0,∀ x ∈ R ⇔m.sin⁡x ≤ 1,∀ x ∈R

Trường hợp 1: m = 0 ta có 0 ≤ 1,∀ x ∈ R. Vậy hàm số đồng biến trên R.

Trường hợp 2: m>0 ta có sin⁡x ≤ 1/m,∀ x ∈ R ⇔ 1/m ≥ 1 ⇔ m ≤ 1

Trường hợp 3: m<0 ta có sin⁡x ≥ 1/m,∀ x ∈ R ⇔ 1/m ≤ -1 ⇔ m ≥ -1

Vậy |m| ≤ 1.

Câu 9: Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = (m - 3)x - (2m + 1).cos⁡x luôn nghịch biến trên R?

    A. -4 ≤ m ≤ 2/3    B. m ≥ 2    C. 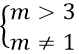   D. m ≤ 2

Lời giải:

Đáp án: A

Giải thích :

Tập xác định: D = R. Ta có y' = m - 3 + (2m + 1)sin x

Hàm số nghịch biến trên R ⇔ y' ≤ 0,∀ x ∈ R ⇔ (2m + 1).sin⁡x ≤ 3 - m,∀ x ∈ R

Trường hợp 1: m =-1/2 ta có 0 ≤ 7/2,∀ x ∈ R. Vậy hàm số nghịch biến trên R.

Trường hợp 2: m<-1/2 ta có sin⁡x ≥ (3 - m)/(2m + 1),∀ x ∈ R ⇔ (3 - m)/(2m + 1) ≤ -1

⇔3 - m ≥ -2m - 1 ⇔ m ≥ -4

Trường hợp 3: m > -1/2 ta có sin⁡ x ≤ (3 - m)/(2m + 1),∀ x ∈ R ⇔ (3 - m)/(2m + 1) ≥ 1

⇔ 3 - m ≥ 2m + 1 ⇔ m ≤ 2/3

Vậy m⇔[-4; 2/3].

Câu 10: Tìm giá trị nhỏ nhất của tham số m sao cho hàm số 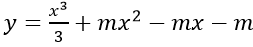luôn đồng biến trên R.

   A. m = -5

   B. m = 0

   C. m = -1

   D. m = -6

Lời giải:

Đáp án: C

Giải thích :

Tập xác định D = R. Ta có y' = x² + 2mx - m

Hàm số đồng biến trên R

Vậy giá trị nhỏ nhất của m để hàm số đồng biển trên R là m = -1.

Câu 11: Hỏi có bao nhiêu giá trị nguyên của tham số m sao cho hàm số y= 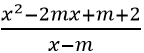đồng biến trên từng khoảng xác định của nó.

   A. 2

   B. 4

   C. Vô số

   D. 0

Lời giải:

Đáp án: C

Giải thích:

Tập xác định D = R\{m}. Ta có y' = (x² - 2mx + 2m² - m - 2)/(x - m)² =(g(x))/(x - m)²

Để hàm số đồng biến trên từng khoảng xác định của nó khi và chỉ khi g(x)≥0,∀ x∈D

Vậy có vô số giá trị nguyên của m thỏa mãn yêu cầu bài toán.

Câu 12: Tìm mối liên hệ giữa các tham số a và b sao cho hàm số

y = f(x) = 2x + a.sin⁡x + b.cos⁡x luôn tăng trên R.

   A. 1/a + 1/b = 1

   B. a + 2b = 2√4

   C. a² + b² ≤ 4

   D. a + 2b ≥ (1 + √2)/3

Lời giải:

Đáp án: C

Giải thích :

Tập xác định D = R. Ta có y' = 2 + a.cos⁡x - b.sin⁡x

Áp dụng bất đẳng thức Schwartz ta có 2 - √(a²+b² ) ≤ y' ≤ 2 + √(a² + b² )

Yêu cầu bài toán đưa đến giải bất phương trình:

y' ≥ 0,∀ x ∈ R ⇔ 2 - √(a²+b² ) ≥ 0  a² + b² ≤ 4