Tính S là tổng tất cả các nghiệm của phương trình 4( 2^2x + 2^-2x) – 4( 2^x + 2^-x) - 7 = 0

Câu hỏi:

Tính S là tổng tất cả các nghiệm của phương trình 4( 2^2x+ 2^-2x)– 4( 2^x+ 2^-x) - 7 = 0.

A. S = 1

B. S = -1

C. S = 3

D. S = 0

Trả lời:

Chọn D.

Đặt t = 2^x+ 2^-x, suy ra t²= 2^2x+ 2^-2x+ 2.

Ta có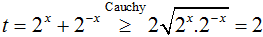

Phương trình trở thành

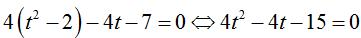
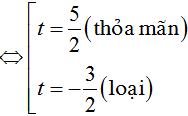
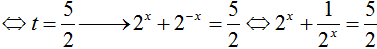
khi đó ; S = x₁+ x₂= 0.

Câu 1:

Xét các số thực dương thỏa mãn $\log_{3} \frac{1 - x y}{x + 2 y} = 3 x y + x + 2 y - 4$ . Tìm giá trị nhỏ nhất S_min của S = x + y

Câu 2:

Cho hai số thực dương a; b thỏa mãn log₂(a + 1) + log₂(b + 1) ≥ 6 Giá trị nhỏ nhất của biểu thức S = a + b là

Câu 3:

Xét các số thực a; b thỏa mãn a > b > 1 Tìm giá trị nhỏ nhất P_min của biểu thức $P = \log_{\frac{a}{b}}^{2} (a^{2}) + 3 \log_{b} \frac{a}{b}$

Câu 4:

Số nghiệm của phương trình: $9^{x + \log_{3} 2} - 2 = 3^{x + \log_{3} 2}$ là

Câu 5:

Biết rằng phương trình $4^{\log_{2} 2 x} - x^{\log_{2} 6} = 2 . 3^{\log_{2} 4 x^{2}}$ có nghiệm duy nhất x = x₀. Mệnh đề nào sau đây là đúng?

Câu 6:

Phương trình 3.25^x-2+ (3x - 10) .5^x-2+ 3 – x = 0 có tất cả bao nhiêu nghiệm?

Câu 7:

Biết phương trình 2^x+1. 5^x= 15 có nghiệm duy nhất dạng alog5 + blog3 + clog2 với a; b; c nguyên . Tính S = a + 2b + 3c.

Câu 8:

Phương trình $2^{x - 3} = 3^{x^{2} - 5 x + 6}$ có hai nghiệm $S = (- 1; \sqrt{5})$ trong đó x₁< x₂, hãy chọn phát biểu đúng

Các dạng bài tập Toán lớp 12