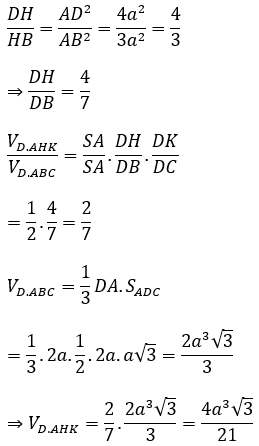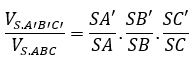Cách tính tỉ số thể tích hai khối chóp cực hay - Toán lớp 12
Cách tính tỉ số thể tích hai khối chóp cực hay
Với Cách tính tỉ số thể tích hai khối chóp cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính tỉ số thể tích hai khối chóp từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ
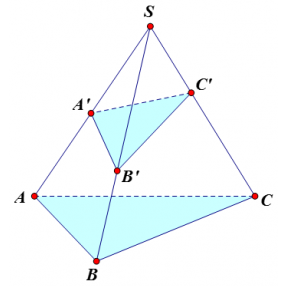
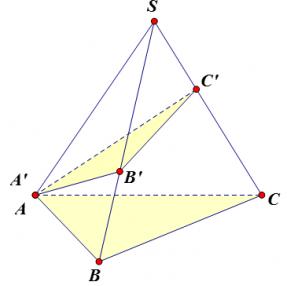
Cho hình chóp S.ABC có 3 điểm A’. B’, C’ lần lượt nằm trên 3 cạnh SA, SB, SC. Khi đó, ta có công thức về tỷ số thể tích như sau:
Chú ý 1:
+ Công thức tỷ số thể tích trên ta chỉ áp dụng cho chóp có đáy là tam giác.
+ Công thức trên vẫn đúng trong trường hợp A’ trùng với A. Khi đó:
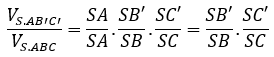
Chú ý 2: (Áp dụng cho khối chóp với mọi đáy)
+ Hai hình chóp có cùng chiều cao thì tỉ số thể tích chính là tỉ số diện tích đáy tương ứng.
+ Hai hình chóp có cùng diện tích đáy thì tỉ số thể tích chính là tỉ số đường cao tương ứng.
Ví dụ minh họa
Bài 1: Hình chóp S.ABC có A’, B’, C’ lần lượt là trung điểm của SA, SB, SC. Tính tỷ số thể tích của hai khối chóp S.A’B’C’ và S.ABC
Hướng dẫn:
Do A’, B’, C’ lần lượt là trung điểm của SA, SB, SC nên ta có:
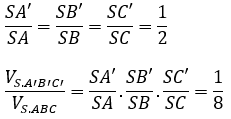
Bài 2: Cho hình chóp tứ giác đều S.ABCD. Gọi A’, B’, C’, D’ theo thứ tự là trung điểm của AB, BC, CD, DA. Khi đó, tỉ số thể tích của hai khối chóp S.A’B’C’D’ và S.ABCD bằng?
Hướng dẫn:
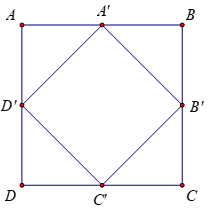
Ta thấy hai hình chóp S.A’B’C’D’ và S.ABCD có chung chiều cao kẻ từ đỉnh S xuống đáy. Vậy để tìm tỉ số thể tích hai khối chóp, ta chỉ cần tìm tỉ số diện tích 2 đáy.
Ta có:
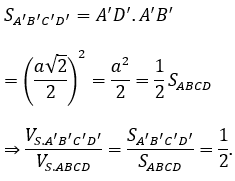
Bài 3: Cho hình chóp SABC. Trên 3 cạnh SA, SB, SC lần lượt lấy 3 điểm M, N, P, sao cho SA=2SM;SB=3SN;SC=2SP.
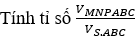
Hướng dẫn:
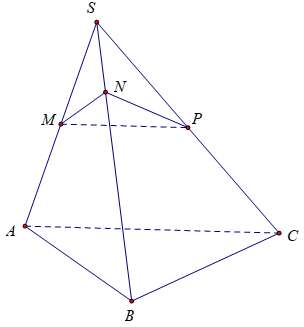
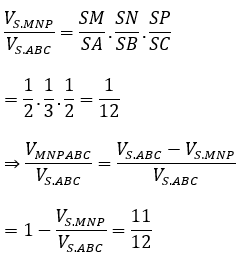
Ta có:
Bài 4: Cho hình chóp S.ABCD có thể tích bằng 48 và ABCD là hình thoi. Các điểm M, N, P, Q lần lượt là các điểm trên các đoạn SA, SB, SC, SD thỏa mãn SA = 2SM; SB = 3SN; SC = 4 SP; SD = 5 SQ. Tính thể tích của khối chóp S.MNPQ
Hướng dẫn:
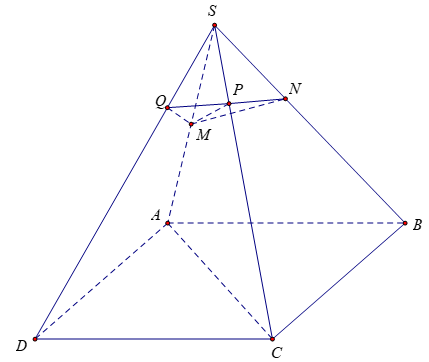
Vì công thức thể tích chỉ dùng cho tam giác có chung đỉnh và tương ứng tỉ lệ cạnh
Nên ta chia khối chóp thành 2 khối chóp nhỏ có đáy là tam giác
Ta có:
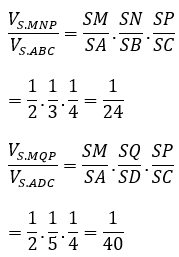
Do ABCD là hình thoi nên SABC = SADC và hai hình chóp S.ABC; S.ADC có cùng chiều cao hạ từ S nên
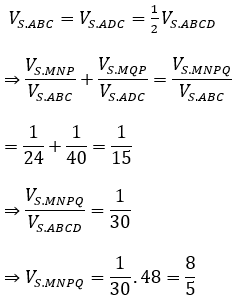
Bài 5: Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân ở B, AC=a√2;SA=a,SA⊥(ABC). Gọi G là trọng tâm của ∆SBC, một mặt phẳng (α) đi qua AG và song song với BC cắt SC, SB lần lượt taị M, N. Tính thể tích khối chóp S.AMN.
Hướng dẫn:
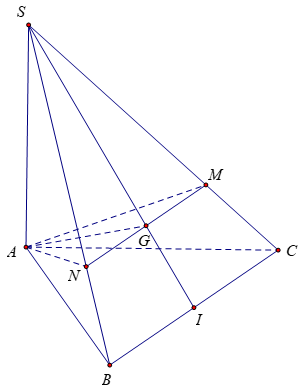
Tam giác ABC vuông tại B có AC=a√2⇒AB=BC=a
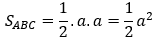
Gọi I là trung điểm của BC, G là trọng tâm tam giác SBC
⇒SG/SI=2/3
Mà MN // BC nên ta có:
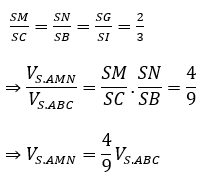
Mặt khác:
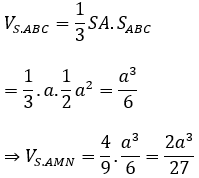
B. Bài tập vận dụng
Bài 1: Cho khối chóp S.ABC. Lấy A’, B’ lần lượt thuộc SA, SB sao cho 2SA’ = 3A’A, 3SB’ = B’B. Tỉ số thể tích giữa hai khối chóp S.A’B’C và S.ABC là:
A.3/20 B.2/15 C.1/6 D.3/10
Lời giải:
Đáp án : A
Giải thích :
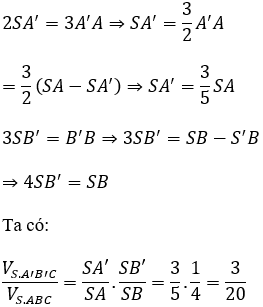
Bài 2: Hình chóp S.ABC có đáy SA vuông góc với đáy, SA=A, AC=a√2, AB = 3a. Gọi M, N là hình chiếu vuông góc của A lên các cạnh SB, SC.
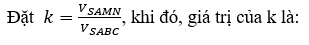
A.1/√30 B.1/3 C.1/30 D.1/2
Lời giải:
Đáp án : C
Giải thích :
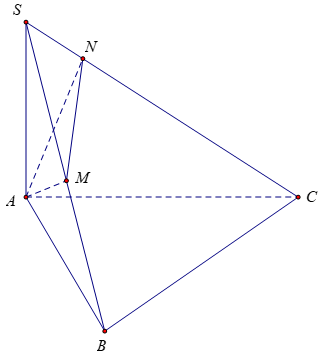
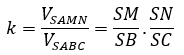
∆SAC vuông tại A, có AN ⊥ SC tại N nên:
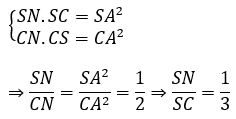
Tương tự, ta có:
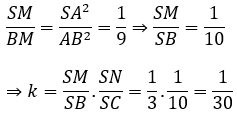
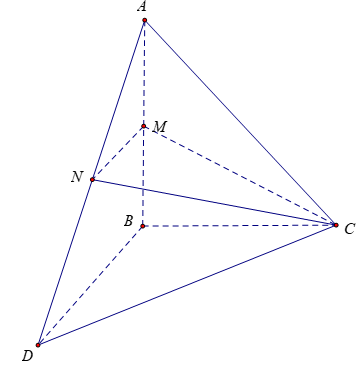
Bài 3: Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau. BA = 3a, BC = BD = 2a. Gọi M, B lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp C.BDNM.
A.8a3 B.(2a3)/3 C.a3 D.(3a3)/2
Lời giải:
Đáp án : D
Giải thích :

Bài 4: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là trung điểm của SB và G là trọng tâm của tam giác SBc. Gọi V, V’ lần lượt là thể tích các khối chóp M.ABC và G.ABD. Tính tỉ số V/V’
A.3/2 B.4/3 C.5/3 D.2
Lời giải:
Đáp án : A
Giải thích :
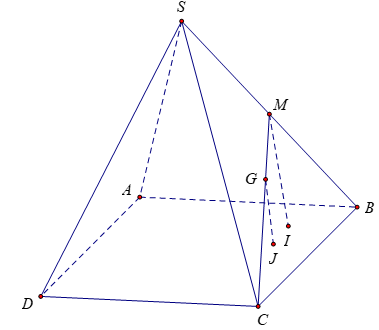
Gọi I, J lần lượt là hình chiếu vuông góc của M, G lên mặt phẳng (ABCD).
Ta có MI // GJ
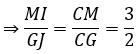
Do các tam giác ABC và ADB có cùng diện tích nên tỉ số thể tích giữa các khối chóp M.ABC và G.ABD là tỉ số đường cao của chúng
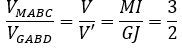
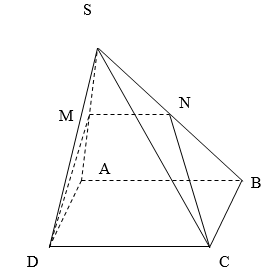
Bài 5: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D. SA vuông góc với mặt đáy (ABCD); AB = 2a, AD = CD = a. Góc giữa mặt phẳng (SBC) và mặt đáy (ABCD) là 60º. Mặt phẳng (P) đi qua CD và trọng tâm G của tam giác SAB cắt các cạnh SA, SB lần lượt tại M và N. Tính thể tích khối chóp S.CDMN theo a.
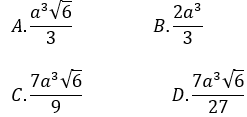
Lời giải:
Đáp án : D
Giải thích :
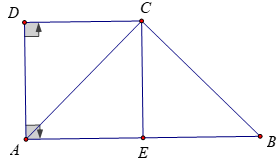
Xét hình thang ABCD vuông tại A, D có AD = DC = a, AB = 2a
Gọi E là trung điểm của AB ⇒ CE=EB=a; CE ⊥ AB
⇒ ∆ACB vuông tại C ⇒ AC ⊥ CB
Ta có:
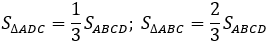

Do các khối chóp S.CDA; S.ABC và S.ABCD có cùng chiều cao hạ từ đỉnh S;
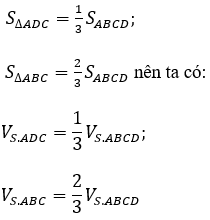
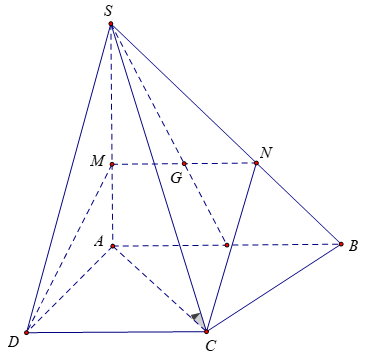
Mặt phẳng (P) đi qua CD và trọng tâm G của tam giác SAB, cắt các cạnh SA, SB lần lượt tại M, N. Khi đó MN // AB và:
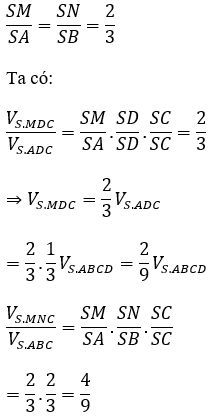
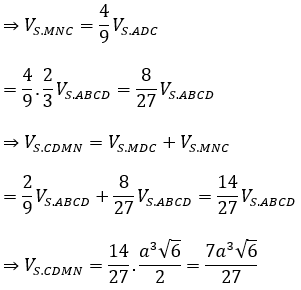
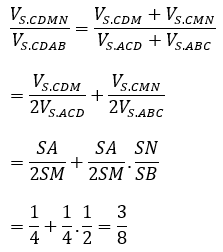
Bài 6: Cho khối chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N theo thứ tự là trung điểm của SA, SB.
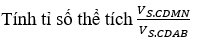
A.1/2 B.3/8 C.5/8 D.1/4
Lời giải:
Đáp án : B
Giải thích :
Bài 7: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA ⊥ (ABC) và SA = 2a. Gọi M, N, P lần lượt là trung điểm của SB, BC, SC. Thể tích khối chóp A.MNP là:
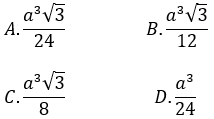
Lời giải:
Đáp án : A
Giải thích :
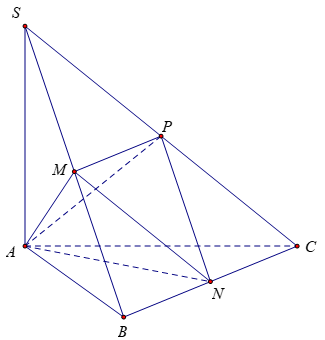
Vì M, N, P lần lượt là trung điểm của SB, SC, BC nên:
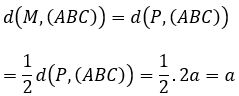
Do ∆ABC đều nên
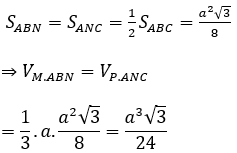
Lại có:
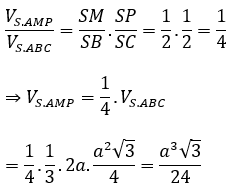
Khi đó:
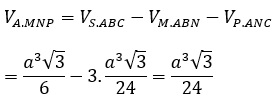
Bài 8: Cho hình chóp S.ABC có các cạnh lần lượt là SA = a, SB = b, SC = c. Trên SA, SB, SC lấy các điểm M, N, P sao cho SM = 1, SN = 2, SP=1/2. Tỷ số thể tích giữa khối chóp S.ABC và S.MNP là:
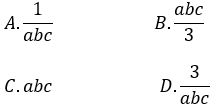
Lời giải:
Đáp án : C
Giải thích :
Áp dụng công thức tỉ lệ thể tích, ta có:
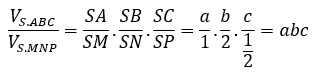
Bài 9: Cho tứ diện ABCD có thể tích bằng V. Gọi B’, D’ lần lượt là trung điểm của các cạnh AB và AD. Mặt phẳng (CB’D’) chia khối tứ diện thành hai phần. Tính tỉ số thể tích hai phần đó.
A.1/6 B.1/9 C.1/12 D.1/3
Lời giải:
Đáp án : D
Giải thích :
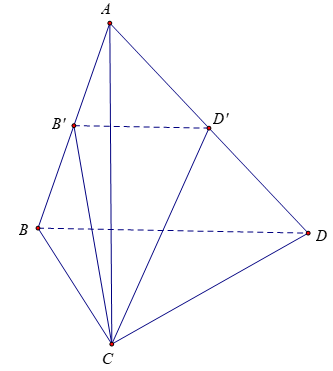
Áp dụng công thức thể tích, ta có:
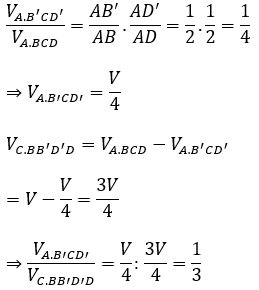
Bài 10: Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, AB=a√3;AC=2a,AD=2a. Gọi H, K lần lượt là hình chiếu của A trên DB, DC. Tính thể tích của tứ diện AHKD
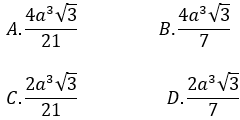
Lời giải:
Đáp án : A
Giải thích :
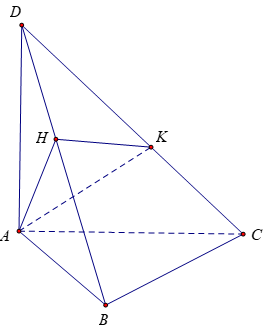
Xét tam giác DAC vuông tại A, AK ⊥ DC có:
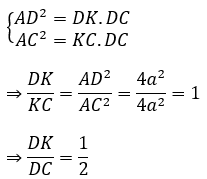
Tương tự, ta có: