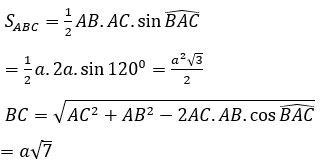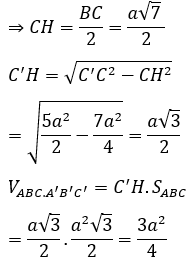Cách tính thể tích khối lăng trụ xiên cực hay - Toán lớp 12

---

Cách tính thể tích khối lăng trụ xiên cực hay

Với Cách tính thể tích khối lăng trụ xiên cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính thể tích khối lăng trụ xiên từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

A. Phương pháp giải & Ví dụ

Hình lăng trụ xiên là hình lăng trụ có cạnh bên không vuông góc với đáy.

Ví dụ minh họa

Bài 1: Cho hình lăng trụ ABC.A’B’C’, ∆ABC đều có cạnh bằng a, AA’ = a và đỉnh A’ cách đều A, B, C. Tính thể tích khối lăng trụ ABC.A’B’C’

Hướng dẫn:

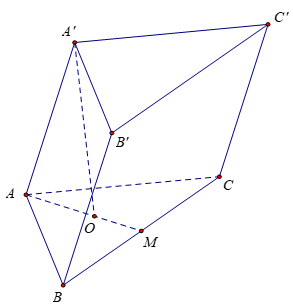
Gọi M là trung điểm của AB, O là tâm của tam giác đều ABC.

Do A’ cách đều các điểm A, B, C nên A'O ⊥ (ABC)

Tam giác ABC đều cạnh a nên:

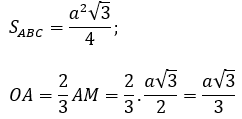
Xét ∆A’AO vuông tại O có:

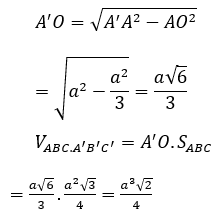
Bài 2: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = a, ∠(ACB) =30⁰; M là trung điểm cạnh AC. Góc giữa cạnh bên và mặt đáy của lăng trụ bằng 60⁰. Hình chiếu vuông góc của đỉnh A’ lên mặt phẳng (ABC) là trung điểm H của BM. Tính thể tích khối lăng trụ ABC.A’B’C’

Hướng dẫn:

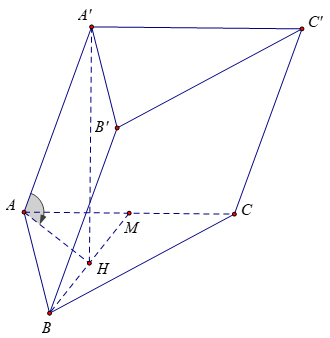
A'H ⊥ (ABC) nên A’H là đường cao của lăng trụ

AH là hình chiếu vuông góc của AA’ lên mặt (ABC) nên góc giữa AA’ và (ABC) là góc (A'AH)=60⁰

∆ABC vuông tại B có AB = a, ∠(ACB)=30⁰

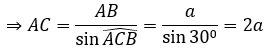
BM là trung tuyến

⇒BM=AM=AC/2=a

⇒BM=AM=AB=a

Do đó ∆ABM đều cạnh a có AH ⊥ BM

⇒AH=(a√3)/2

Xét tam giác AA’H có:

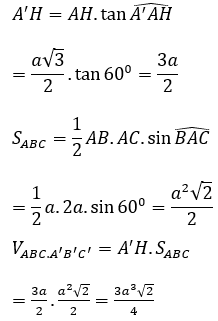
Bài 3: Cho hình lăng trụ ABC.A’B’C’, đáy ABC có AC = a√3, BC = 3a, ∠(ACB)=30⁰. Cạnh bên hợp với mặt phẳng đáy góc 60⁰ và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho HC = 3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Tính thể tích khối lăng trụ ABC.A’B’C’

Hướng dẫn:

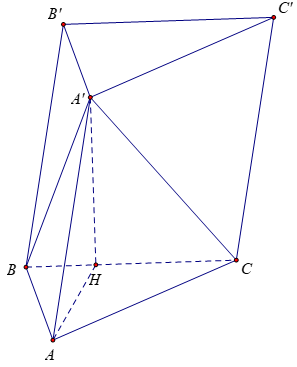
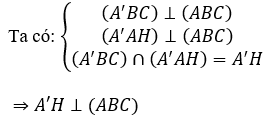
⇒AH là hình chiếu vuông góc của AA’ lên (ABCD)

Khi đó góc giữa AA’ và (ABCD) là góc (A'AH) =60⁰

Ta có: BC = 3a, HC = 3BH ⇒ HC=9a/4

Xét tam giác ACH có:

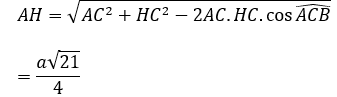
Xét tam giác AA’H có:

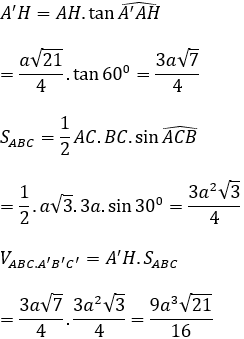
Bài 4: Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh a. Chân đường vuông góc kẻ từ A’ lên (ABCD) trùng với giao điểm của 2 đường chéo đáy, mặt (AA’B’B) hợp với đáy một góc 60°. Tính thể tích khối lăng trụ ABCD.A’B’C’D’.

Hướng dẫn:

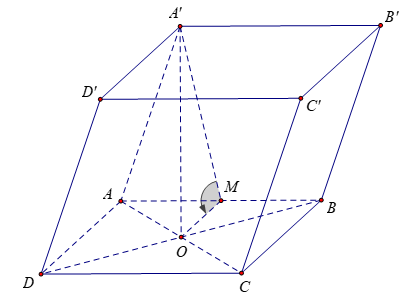
Kẻ OM ⊥ AB⇒ OM là đường trung bình của tam giác ABC

⇒ OM=AB/2=a/2

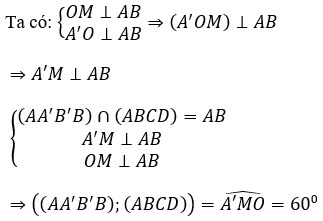
Xét tam giác A’MO có:

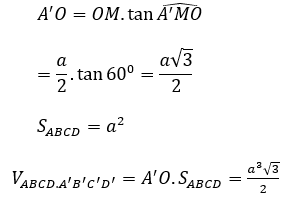
Bài 5: Cho lăng trụ ABC.A’B’C’ có độ dài tất cả các cạnh bằng a và hình chiếu của đỉnh C trên mặt phẳng (ABB’A’) là tâm của hình bình hành ABB’A’. Tính thể tích của khối lăng trụ.

Hướng dẫn:

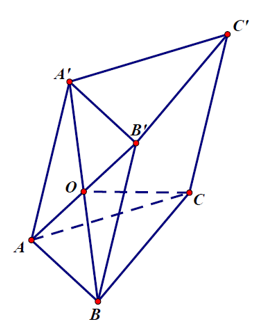
Gọi O là tâm hình bình hành ABB’A’.

Ta có CO ⊥ (ABB' A')

Vì CA = CB nên , suy ra hình thoi ABB’A’ là hình vuông

Do đó:

OA=AB/√2=a/√2

Xét tam giác COA vuông tại O có:

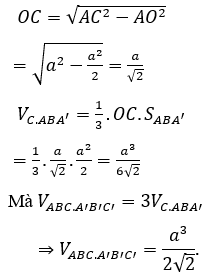
B. Bài tập vận dụng

Bài 1: Cho hình lăng trụ ABC.A’B’C’có AB = 2a, AC = a, AA'=(a√10)/2; ∠(BAC) =120º . Hình chiếu vuông góc của C’ lên mặt phẳng (ABC) là trung điểm của cạnh BC. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a

Lời giải:

Đáp án : B

Giải thích :

Gọi H là trung điểm BC. Từ giả thiết suy ra C'H ⊥ (ABC).

Trong ∆ABC ta có:

Bài 2: Cho hình lăng trụ ABCD.A’B’C’D’có đáy ABCD là hình vuông cạnh bằng a. Hình chiếu vuông góc của điểm A’ trên mặt phẳng ABCD là trung điểm I của cạnh AB. Biết A’C tạo với mặt phẳng đáy một góc α với tan⁡α=2/√5 . Thể tích khối chóp A’.ICD là

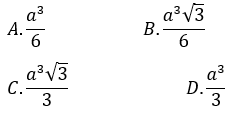
Lời giải:

Đáp án : D

Giải thích :

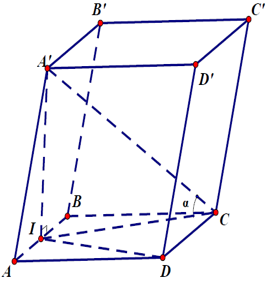
Từ giả thiết ta có A' I ⊥ (ABCD)

Theo bài ta có IC là hình chiếu vuông góc của A’C trên mặt phẳng (ABCD).

Khi đó góc giữa đường thẳng A’C và (ABCD) là góc giữa A’C và IC

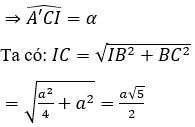
Xét tam giác vuông A’IC có:

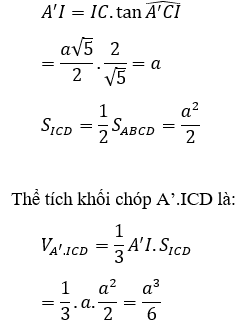
Bài 3: Cho hình lăng trụ tam giác ABC.A’B’C’có BB’ = a góc giữa đường thẳng BB’ và mặt phẳng (ABC) bằng 60º, tam giác ABC vuông tại C và ∠(BAC) =60º. Hình chiếu vuông góc của điểm B’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Thể tích khối tứ diện A’ABC là

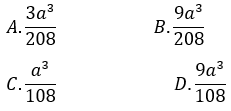
Lời giải:

Đáp án : B

Giải thích :

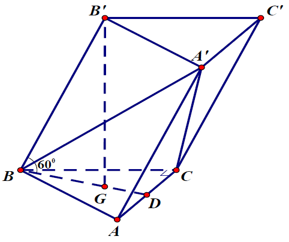
Gọi D là trung điểm AC, G là trọng tâm tam giác ABC

⇒ B'G ⊥ (ABC)

Ta có BG là hình chiếu vuông góc của BB’ trên (ABC)

⇒ Góc giữa BB’ và (ABC) là góc giữa BB’ và BG

⇒ ∠(B'BG)=60º

Xét tam giác B’BG vuông tại G có:

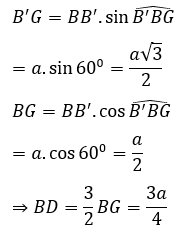
Trong tam giác ABC có:

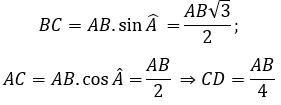
Xét tam giác BCD vuông tại C có:

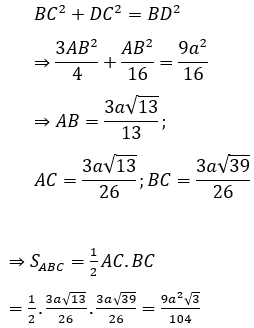
Thể tích khối tứ diện A’ABC là :

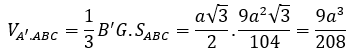
Bài 4: Cho lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A’ lên mặt phẳng (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC. Cho ∠(BAA' ) =45º .Thể tích khối lăng trụ đã cho là

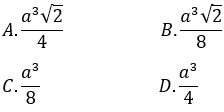
Lời giải:

Đáp án : B

Giải thích :

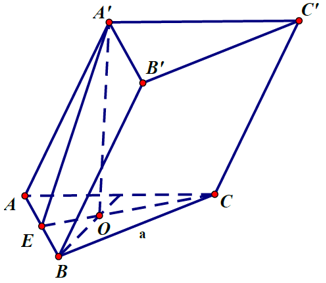
Gọi E là trung điểm của AB, ta có :

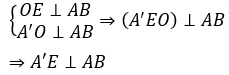
Tam giác vuông A’EA có A = 45º nên là tam giác vuông cân tại E.

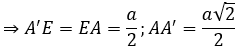
Tam giác ABC đều cạnh a có:

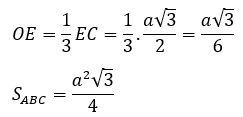
Tam giác vuông A’OE ( vuông tại O) có:

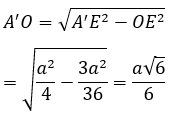
Thể tích của khối lăng trụ ABC.A’B’C’:

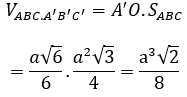
Bài 5: Cho hình hộp ABCD.A’B’C’D’ có đáy là hình chữ nhật với AB=√3; AD=√7. Hai mặt bên (ABB’A’) và (ADD’A’) lần lượt tạo với đáy những góc 45º và 60º. Tính thể tích khối hộp nếu biết cạnh bên bằng 1.

A. 3        B. 2        C. 4        D. 8

Lời giải:

Đáp án : A

Giải thích :

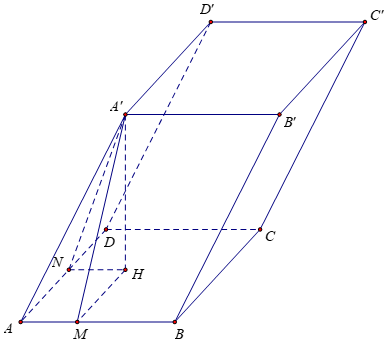
Kẻ A' H ⊥ (ABCD); HM ⊥ AB; HN ⊥ AD

Ta có: A' H ⊥ AB; HM ⊥ AB ⇒ (A' MH) ⊥ AB

⇒ A'M ⊥ AB

Khi đó, góc giữa mặt phẳng (ABB’A’) và (ABCD) là góc giữa A’M và MH

⇒ ∠(A'MH)=45º

Tương tự, ta có: góc giữa mặt phẳng (ABD’A’) và (ABCD) là góc giữa A’N và NH

⇒ ∠(A'NH)=60º

Đặt A’H = x .Khi đó :

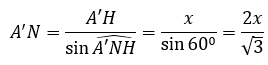
Xét tam giác ANA’vuông tại N có :

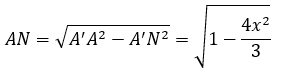
Xét tam giác A’HM vuông tại H có : HM=A' H.tan⁡∠(A'MH) =x.tan⁡45º =x

Mà AN = HM (ANHM là hình chữ nhật)

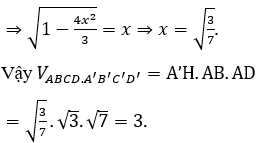
Bài 6: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên (AA’C’C) tạo với đáy một góc 45°. Tính thể tích khối lăng trụ.

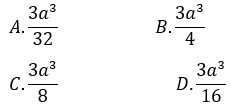
Lời giải:

Đáp án : D

Giải thích :

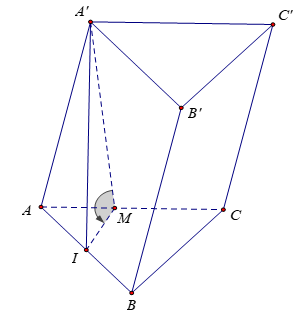
Gọi I là trung điểm của AB ⇒ A' I ⊥ (ABC)

Kẻ IM ⊥ AC

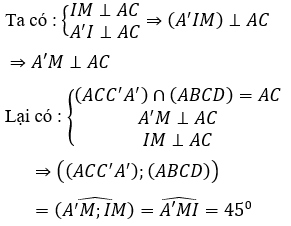
Xét tam giác AMI vuông tại M có :

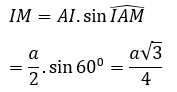
Xét tam giác A’IM vuông tại I có :

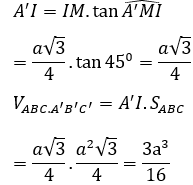
Bài 7: Cho lăng trụ xiên tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, biết cạnh bên là a√3 và hợp với đáy ABC một góc 60°. Tính thể tích lăng trụ.

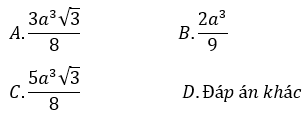
Lời giải:

Đáp án : A

Giải thích :

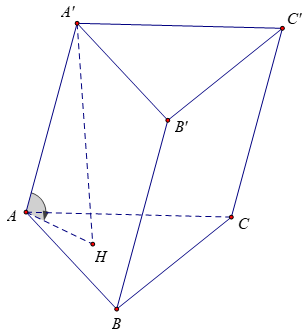
Gọi H là hình chiếu vuông góc của A’ lên (ABC).

Ta có: AH là hình chiếu vuông góc của AA’ lên (ABC)

⇒ Góc giữa AA’ và (ABC) là góc giữa AH và AA’

⇒ ∠(A'AH)=60º

Xét tam giác AA’H vuông tại H có:

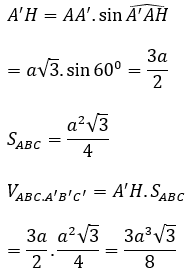
Bài 8: Cho hình lăng trụ tam giác ABC.A’B’C’ có thể tích là V. Gọi I, J lần lượt là trung điểm cạnh AA’ và BB’. Khi đó thể tích của khối đa diện ABCIJC’ bằng:

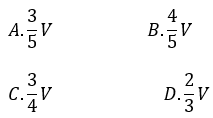
Lời giải:

Đáp án : D

Giải thích :

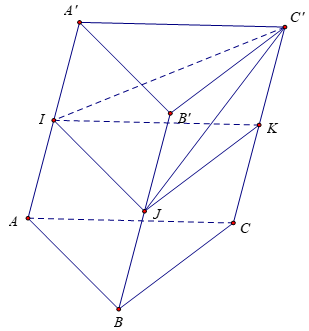
Gọi K là trung điểm của CC’ .

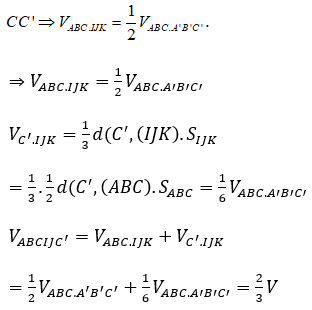
Bài 9: Cho hình hộp ABCD.A’B’C’D’, O là giao điểm của AC và BD. Tỷ số thể tích của khối chóp O.A’B’C’D’ và khối hộp ABCD.A’B’C’D’ là:

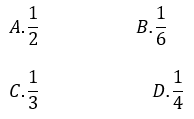
Lời giải:

Đáp án : C

Giải thích :

Ta có:

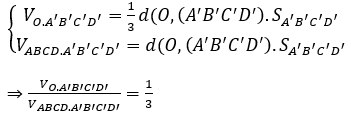
Bài 10: Cho lăng trụ A BC.A’B’C’ có đáy là tam giác đều cạnh a, hình chiếu của A’ lên (ABC) trùng với trung điểm của BC. Thể tích của khối lăng trụ là (a³√3)/8, độ dài cạnh bên của khối lăng trụ là:

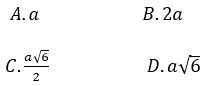
Lời giải:

Đáp án : A

Giải thích :

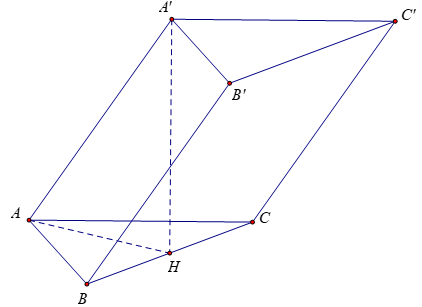
Gọi H trung điểm của BC ⇒ A'H ⊥ (ABC)

Ta có: V_ABC.A'B'C' = A' H.S_ABC

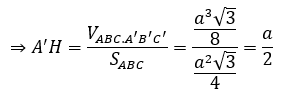
Lại có AH là đường trung tuyến của tam giác đều cạnh a

⇒ AH=(a√3)/2

Xét tam giác A’AH vuông tại H có:

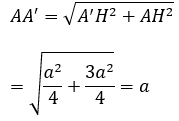
Vậy cạnh bên bằng a.