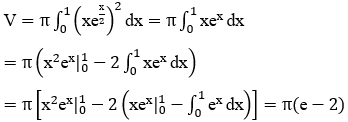Ứng dụng của tích phân: Tính thể tích khối tròn xoay - Toán lớp 12
Ứng dụng của tích phân: Tính thể tích khối tròn xoay
Với Ứng dụng của tích phân: Tính thể tích khối tròn xoay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Ứng dụng của tích phân: Tính thể tích khối tròn xoay từ đó đạt điểm cao trong bài thi môn Toán lớp 12.
A. Phương pháp giải & Ví dụ
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x, (a ≤ x ≤ b). Giả sử S(x) là hàm số liên tục trên đoạn [a;b].
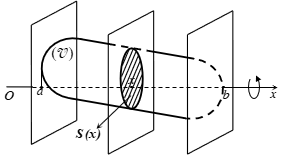
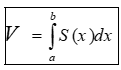
Bài toán 1: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y=f(x), trục hoành và hai đường thẳng x=a, x=b quanh trục Ox:
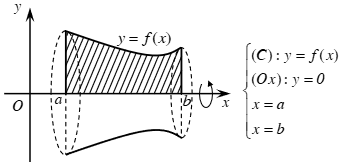
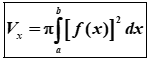
Bài toán 2: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x=g(y), trục hoành và hai đường thẳng y=c, y=d quanh trục Oy:
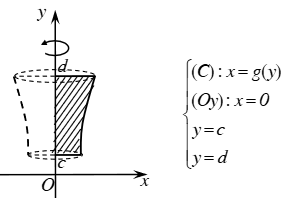
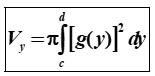
Bài toán 3: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y=f(x), y=g(x) và hai đường thẳng x=a, x=b quanh trục Ox:
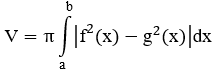
Ví dụ minh họa
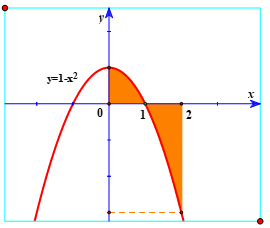
Bài 1: Tính thể tích khối tròn xoay được giới hạn bởi các đường y=(1-x2 ), y=0, x=0 và x=2 khi quay quanh trục Ox.
Hướng dẫn:
Thể tích khối tròn xoay được giới hạn bởi các đường
y = (1-x2), y=0, x=0 và x=2 khi quay quanh trục Ox là:
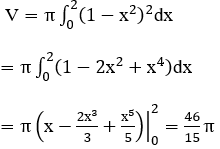
Bài 2: Cho hình phẳng giới hạn bởi các đường y=√x; y=x quay quanh trục Ox. Tính thể tích khối tròn xoay tạo.
Hướng dẫn:
Giải phương trình √x = x ⇔ x ∈ {0;1}.
Thể tích khối tròn xoay giới hạn bởi các đường y=√x;y=x khi quay quanh trục Ox là
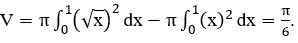
Bài 3: Gọi (H) là hình phẳng giới hạn bởi các đường y=tanx; Ox; x=0; x=π/4. Quay (H) xung quanh trục Ox ta được khối tròn xoay có thể tích bằng bao nhiêu?
Hướng dẫn:
Thể tích khối tròn xoay được giới hạn bởi các đường y=tanx; Ox; x=0; x=π/4 là:
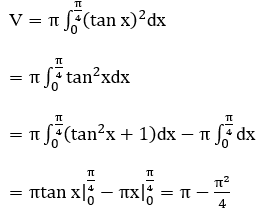
B. Bài tập vận dụng
Bài 1: Tính thể tích khối tròn xoay sinh ra do quay hình phẳng giới hạn bởi các đường y=x3, trục Ox, x=-1, x=1 một vòng quanh trục Ox.
Lời giải:
Thể tích khối tròn xoay được giới hạn bởi các đường y=x3, trục Ox, x=-1, x=1 một vòng quanh trục Ox là:
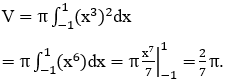
Bài 2: Gọi (H) là hình phẳng giới hạn bởi các đường y=2x-x2; Ox. Quay (H) xung quanh trục Ox ta được khối tròn xoay. Tính thể tích của (H)
Lời giải:
Phương trình hoành độ giao điểm:
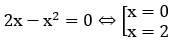
Suy ra
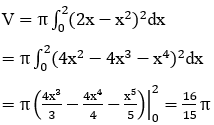
Bài 3: Tính thể tích khối tròn xoay giới hạn bởi y=lnx,y=0,x=e quay quanh trục Ox.
Lời giải:
Phương trình hoành độ giao điểm: lnx=0 ⇔ x=1
Khi đó thể tích cần tìm là:
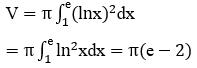
Bài 4: Cho hình phẳng (H) được giới hạn bởi đường cong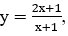 
trục Ox và trục Oy. Tính thể tích của khối tròn xoay khi cho hình (H) quay quanh trục Ox .
Lời giải:
Phương trình hoành độ giao điểm:
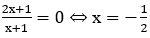
Suy ra
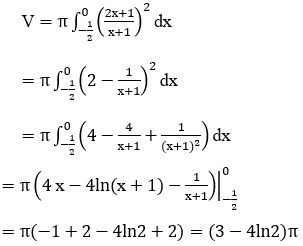
Bài 5: Gọi (H) là hình phẳng giới hạn bởi các đường: y=3x ;y=x ; x=1. Quay (H) xung quanh trục Ox ta được khối tròn xoay. Tính thể tích của khối tròn xoay (H).
Lời giải:
Phương trình hoành độ giao điểm: 3x =x ⇔ x=0.
Suy ra:
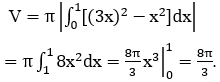
Bài 6: Cho hình (H) giới hạn bởi các đường y=x+1; y=6/x; x=1; x > 0. Quay hình (H) quanh trục Ox ta được khối tròn xoay có thể tích là bao nhiêu?
Lời giải:
Phương trình hoành độ giao điểm: x+1 =6/x ⇔ x2+x-6=0 ⇒ x=2.
Suy ra:
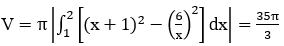
Bài 7: Tính thể tích khối tròn xoay được tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường y=1/cosx, x=0 và x=π/4
Lời giải:
Thể tích khối tròn xoay được tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường y=1/cosx, x=0 và x=π/4 là:
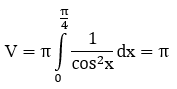
Bài 8: Tính thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường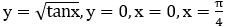 
xung quanh trục Ox.
Lời giải:
Thể tích V của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
y=√tanx, y=0, x=0, x=π/4 xung quanh trục Ox là:
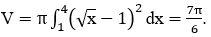
Bài 9: Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y=e2x, y=0, x=0 và x=2. Tính thể tích của khối tròn xoay được tạo thành khi quay (H) xung quanh trục Ox.
Lời giải:
Thể tích khối tròn xoay tạo thành là
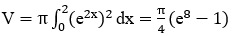
Bài 10: Cho hình phẳng (H) giới hạn bởi các đường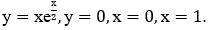 
Tính thể tích của khối tròn xoay được tạo thành khi quay (H) xung quanh trục x .
Lời giải:
Thể tích cần tìm là
