Trắc nghiệm tìm nguyên hàm bằng phương pháp từng phần - Toán lớp 12

---

Trắc nghiệm tìm nguyên hàm bằng phương pháp từng phần

Với Trắc nghiệm tìm nguyên hàm bằng phương pháp từng phần Toán lớp 12 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm nguyên hàm bằng phương pháp từng phần từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Bài 1: Tính F(x) = ∫xcosx dx ta được kết quả:

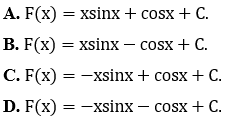
Lời giải:

Đáp án :

Giải thích :

Xét F(x) = ∫xcosx dx

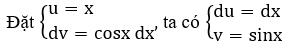
Khi đó F(x) = ∫xcosx dx = xsinx- ∫sinx dx = xsinx+cosx+C

Bài 2: Chọn công thức đúng dùng để tìm họ nguyên hàm F(x) = ∫(x+1)sin2x dx

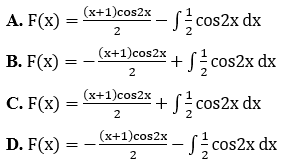
Lời giải:

Đáp án :

Giải thích :

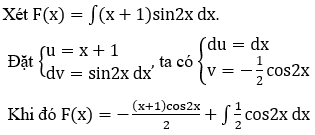
Bài 3: Tìm họ nguyên hàm ∫xe^x dx là:

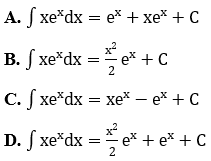
Lời giải:

Đáp án :

Giải thích :

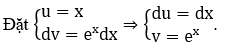
Theo công thức tính nguyên hàm từng phần, ta có

∫xe^x dx = ∫xe^x dx = xe^x- ∫e^x dx = xe^x - ∫d(e^x ) = xe^x-e^x+C

Bài 4: Tính ∫xsin(2x+1)dx ta được kết quả

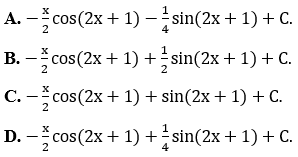
Lời giải:

Đáp án :

Giải thích :

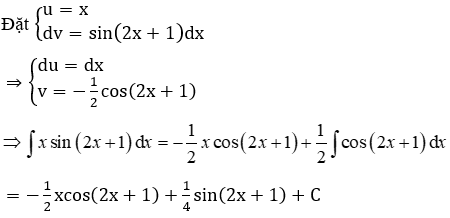
Bài 5: Cho ∫(2x+3) e^x dx. Khẳng định nào sau đây đúng.

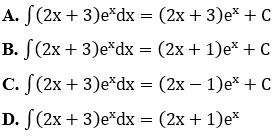
Lời giải:

Đáp án :

Giải thích :

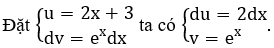
Khi đó

∫(2x+3) e^x dx = (2x+3) e^x - ∫2e^x dx = (2x+3) e^x - 2e^x+C=(2x+1) e^x+C

Bài 6: Họ nguyên hàm của hàm số f(x) = xlnx là:

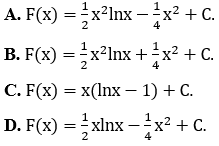
Lời giải:

Đáp án :

Giải thích :

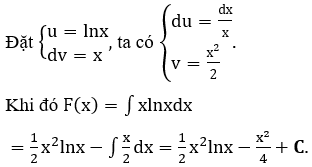
Bài 7: Tìm một nguyên hàm F(x) của hàm số sau

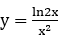
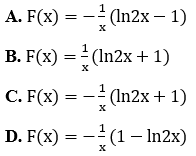
Lời giải:

Đáp án :

Giải thích :

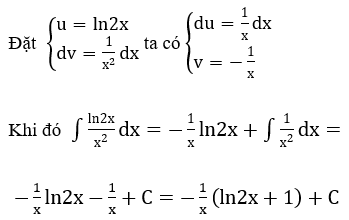
Bài 8: Trong các khẳng định sau, khẳng định nào đúng?

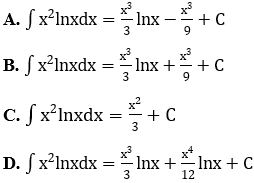
Lời giải:

Đáp án :

Giải thích :

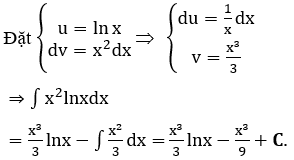
Bài 9: Tính nguyên hàm của hàm số ∫cos√x dx

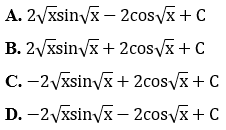
Lời giải:

Đáp án :

Giải thích :

Đặt t = √x ⇒ t² = x ⇒ 2tdt = dx. Ta được ∫cos√x dx = ∫2tcost dt.

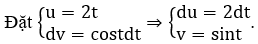
Do đó ∫2tcostdt = 2tsint-2 ∫sintdt = 2tsint + 2cost + C = 2√x sin√x + 2cos√x + C

Bài 10: Tính F(x) = ∫(2x-1) e^1-x dx = e^1-x (Ax+B)+C . Giá trị của biểu thức A+B bằng

Lời giải:

Đáp án :

Giải thích :

Ta có F(x) = ∫(2x-1) e^1-x dx = e^1-x (Ax+B)+C

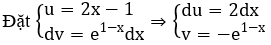
Theo công thức tính nguyên hàm từng phần, ta có

F(x) = -(2x-1) e^1-x + ∫2e^1-x dx = -(2x-1) e^1-x-2e^1-x+C = (-2x-1) e^1-x+C

Vậy A + B = -3.

Bài 11: Cho F(x) = (ax²+bx+c) e^x là một nguyên hàm của f(x) = (x-3)²e^x. Tính S=a+b+c.

Lời giải:

Đáp án :

Giải thích :

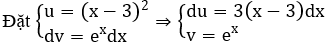
⇒ ∫(x-3)²e^x dx = (x-3)²e^x-2 ∫(x-3) e^x dx

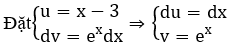
⇒ ∫(x-3)²e^x dx = (x-3)²e^x-2 ∫(x-3) e^x dx=(x-3)²e^x-2[(x-3) e^x- ∫e^x dx] = (x²-8x+17) e^x+C

Mà a=1; b=-8; c=17 ⇒ S=10

Bài 12: Tìm nguyên hàm của hàm số f(x) = x²(3.lnx+1)

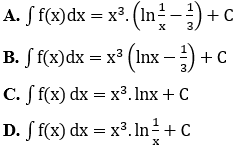
Lời giải:

Đáp án :

Giải thích :

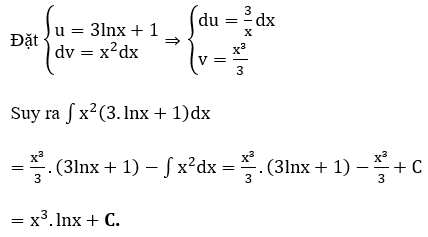
Bài 13: Tìm nguyên hàm H của hàm số f(x) = √x lnx

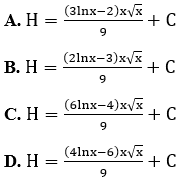
Lời giải:

Đáp án :

Giải thích :

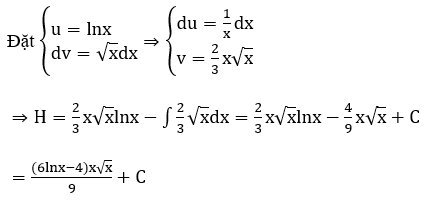
Bài 14: Tìm nguyên hàm H của hàm số f(x) = (3x²+1)lnx

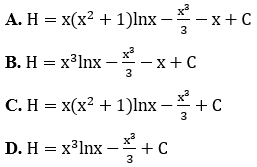
Lời giải:

Đáp án :

Giải thích :

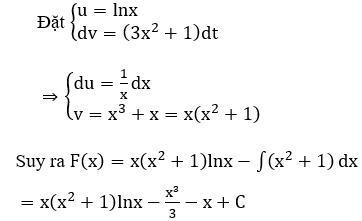
Bài 15: Nguyên hàm của hàm số sau bằng:

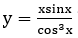
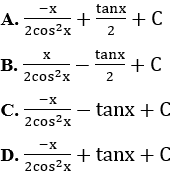
Lời giải:

Đáp án :

Giải thích :