Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có phương trình
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có phương trình đường phân giác trong góc A là: . Biết rằng điểm M (0;5;3) thuộc đường thẳng AB và điểm N (1;1;0) thuộc đường thẳng AC. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng AC.
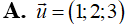

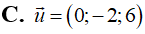
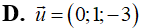
Trả lời:
Chọn B
Phương trình tham số của đường phân giác trong góc 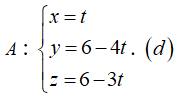
Gọi D là điểm đối xứng với M qua (d). Khi đó D ∈ AC => đường thẳng AC có một vectơ chỉ phương là 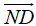 .
.
Ta xác định điểm D.
Gọi K là giao điểm MD với (d). Ta có K (t;6-4t;6-3t); 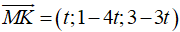

Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;1;1). Viết phương trình mặt phẳng (P) đi qua M và cắt ba tia Ox, Oy, Oz lần lượt tại các điểm A, B, C khác gốc O sao cho thể tích khối tứ diện OABC nhỏ nhất.
Xem lời giải »
Câu 2:
Trong không gian Oxyz, cho hai điểm M (2;2;1), . Viết phương trình mặt cầu có tâm là tâm của đường tròn nội tiếp tam giác OMN và tiếp xúc với mặt phẳng (Oxz).
Xem lời giải »
Câu 3:
Trong không gian Oxyz, Cho mặt phẳng (R): x+y-2z+2=0 và đường thẳng .Đường thẳng Δ2 nằm trong mặt phẳng (R) đồng thời cắt và vuông góc với đường thẳng Δ1 có phương trình là:
Xem lời giải »
Câu 4:
Trong không gian Oxyz, mặt phẳng (α) đi qua M (1;1;4) cắt các tia Ox, Oy, Oz lần lượt tại A, B, C phân biệt sao cho tứ diện OABC có thể tích nhỏ nhất. Tính thể tích nhỏ nhất đó.
Xem lời giải »
Câu 5:
Trong không gian Oxyz, phương trình mặt phẳng (P) song song và cách đều hai đường thẳng , là?
Xem lời giải »
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho điểm A (3;1;0), B (-9;4;9) và mặt phẳng (P) có phương trình 2x-y+z+1=0. Gọi I (a;b;c) là điểm thuộc mặt phẳng (P) sao cho |IA - IB| đạt giá trị lớn nhất. Khi đó tổng a+b+c bằng:
Xem lời giải »
Câu 7:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+y²+ (z+2)²=4 và đường thẳng . Gọi T là tập tất cả các giá trị của m để d cắt (S) tại hai điểm phân biệt A, B sao cho các tiếp diện của (S) tại A và B tạo với nhau góc lớn nhất có thể. Tính tổng các phần tử của tập hợp T.
Xem lời giải »
.

